Use o teorema de Green para encontrar a circulação no sentido anti-horário para o campo e a curva :
: O laço do lado direito da lemniscata .
Passo 1
No enunciado ele já pede pra usar o Teorema de Green, mas mesmo que pudesse escolher, eu nunca faria isso pela definição, imagina como ia ficar complicado parametrizar essa lemniscata...
Por sorte, o teorema simplifica bastante as coisas pra a gente:
Passo 2
Como a fórmula nos mostra, precisamos calcular as derivadas parciais:
Nada muito bizarro por enquanto, né?
Passo 3
Vamos jogando na fórmula, então:
Mas agora não dá pra fugir, vamos ter que ver como que vai ficar esse domínio de .
Passo 4
A fórmula da tal lemniscata (nossa, o que é isso??) já sugere algo com coordenadas polares, então vamos usá-las. (Pra lembrar: )
Primeiro, vamos tentar entender o que é a imagem e, pra isso, vou “marcar” alguns pontos importantes.
A curva começa com , que é o valor máximo para e, partir disso:
é decrescente de até .
não tem valor real definido, já que .
crescente de 0 até 1.
decrescente de 1 até 0
não definido, .
crescente de 0 até 1.
Se você anotou tudo direitinho, acho que chegou perto de algo assim:
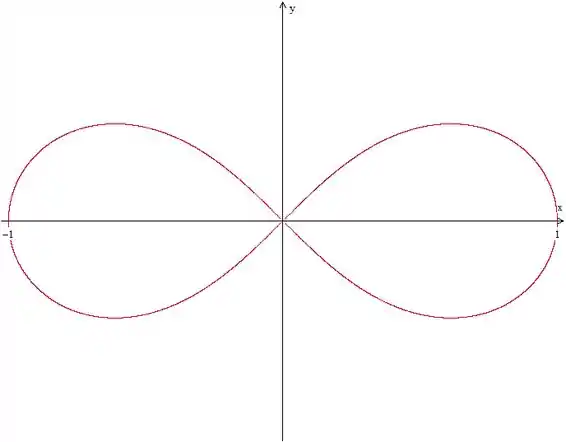
Eu sei, bem complicado, mas o que importa é que encontrar os limites, e agora fica mais tranquilo.
A parte do laço direito que o enunciado se refere deve ser a parte com , mais especificamente, as partes que escrevemos e ; que, pra ficar bonitinho (e bem mais simples), podemos escrever . Opa, já temos um dos limites!
E o outro é bem mais fácil, a região é simplesmente o que está dentro da curva, ou seja, .
Agora é só resolver a integral, vamos ver como vai ficar.
Passo 5
Temos que:
(lembrando que )
Viu? Até que não foi tão complicado assim, chato mesmo foi só entender a curva, mas agora já resolvemos!