Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Green

Ver Teoria
Exercício 481234567891011121314151617181920212223242526272829303132333435363738394041424344454647495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Considere o campo plano

F x ,   y = - y x 2 + y 2 + y , x x 2 + y 2 + e y 2 ,     x ,   y ≠ 0 ,   0 .

e os caminhos:

C =   quadrado de vértices 2 ,   0 ,   0 ,   2 ,   - 2 ,   0 e 0 ,   - 2 com orientação anti-horária;

D =   circunferência unitária com orientação horaria.

Calcule

∫ C   F d r + ∫ D   F d r

Sugestão: use o Teorema de Green (generalizado).

Passo 1

Cara, é super aconselhável iniciarmos esse problema fazendo um esboço das duas curvas para termos uma noção mais ampla do negócio. Então me acompanha!

A primeira curva, C , foi nos dados os pontos, então... marquemos os pontos

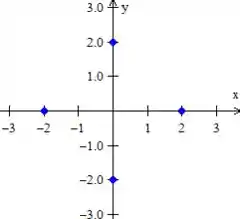
Ligando esses pontos formando o quadrado pedido...

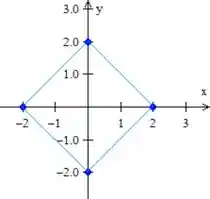
Desenhando também a circunferência unitária...

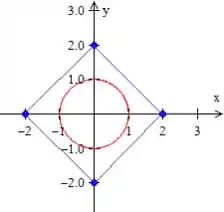
AH! não se esqueça das orientações, heim!

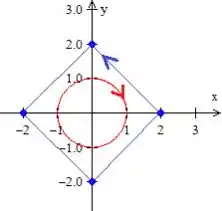
Passo 2

Pow! como vamos trabalhar com o teorema de Green... o que ele fala mesmo?

Ele nos fala que se a gente tem uma região orientada positivamente (curva de fora no sentido anti-horário e as curvas de dentro no sentido horário – exatamente como a nossa :D), e;

sem singularidades na região delimitada por essas curvas (no nosso caso isso se aplica porque o único ponto problemático é a origem, que não está na região entre a curva azul e a vermelha :D);

Podemos relacionar então relacionar,

∫ ∂ R   F d r = ∬ R   ∂ Q ∂ x - ∂ P ∂ y d A

Onde a R é a região entre as duas curvas

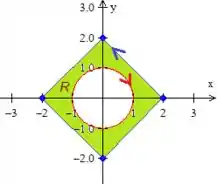
e o ∂ R é a borda da região entre as duas curvas, ou seja, ∂ R = C + D ! Logo

∫ C + D   F d r = ∬ R   ∂ Q ∂ x - ∂ P ∂ y d A     →

∫ C   F d r + ∫ D   F d r = ∬ R   ∂ Q ∂ x - ∂ P ∂ y d A

Pow, então bora calcular esse rotacional aí, integrarmos e ser feliz !

Passo 3

Vamos então calcular aqui o rotacional do campo F , ou seja

∂ Q ∂ x - ∂ P ∂ y

No nosso caso, a gente tem

F x ,   y = - y x 2 + y 2 + y ⏟ P , x x 2 + y 2 + e y 2 ⏟ Q

Calculando então essa primeira derivada parcial aí

∂ Q ∂ x = ∂ x x 2 + y 2 + e y 2 ∂ x   →

Lembrando que a derivada parcial em relação a x , y é tomado como constante...

∂ Q ∂ x = ∂ x x 2 + y 2 ∂ x   →

Agora aqui, não podemos esquecer-nos de derivar aplicando a regra da razão

∂ Q ∂ x = x 2 + y 2 x ' - x ∂ x 2 + y 2 ∂ x x 2 + y 2 2 →

Derivando esses caras do denominador

∂ Q ∂ x = x 2 + y 2 - x 2 x x 2 + y 2 2 =

y 2 - x 2 x 2 + y 2 2

Passo 4

Fazendo o mesmo, mas agora para ∂ P ∂ y :

∂ P ∂ y = ∂ - y x 2 + y 2 + y ∂ y →

derivada da soma é a soma das derivadas...

∂ P ∂ y = ∂ - y x 2 + y 2 ∂ y + ∂ y ∂ y →

∂ P ∂ y = ∂ - y x 2 + y 2 ∂ y + 1

calculando essa primeira derivada aí semelhante como calculamos para x ,

∂ P ∂ x = x 2 + y 2 - y ' - - y ∂ x 2 + y 2 ∂ y x 2 + y 2 2 + 1 →

∂ P ∂ x = - x 2 - y 2 - - y 2 y x 2 + y 2 2 + 1 =

y 2 - x 2 x 2 + y 2 2 + 1

Opa!!! Deu muiiito parecido :D! Isso quer dizer que

∂ Q ∂ x - ∂ P ∂ y = y 2 - x 2 x 2 + y 2 2 - y 2 - x 2 x 2 + y 2 2 + 1

corta e corta...

∂ Q ∂ x - ∂ P ∂ y = - 1

Passo 5

Voltando então para G r e e n

∮ C   F d r + ∮ D   F d r = ∬ R   ∂ Q ∂ x - ∂ P ∂ y d A     →

∮ C   F d r + ∮ D   F d r = ∬ R   - 1 d A →

Epa! (vários “Epa’s!” nessa questão. Assim que é bom hehe :D) Quem é ∬ R   d A mesmo?

Sim! É a área da região R ! :D

∮ C   F d r + ∮ D   F d r = - Á r e a   d e   R

Então vamos procurar a área dessa região aí e mata o problema!

Passo 6

A região R é muito simpática com a gente, pois ela é formada por um quadrado e uma circunferência

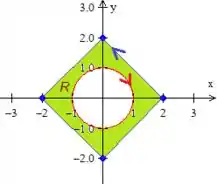
Calculando a área do quadrado por A = l 2 ... Mas espera! quem é o lado l do quadrado?

Pitágoras responde

l 2 = 2 2 + 2 2   →

l 2 = 2 ∙ 2 2  

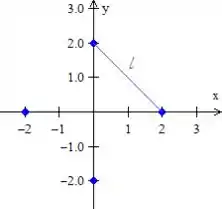
Como a área do quadrado é l 2

A .   q u a d . = l 2 = 8

Quanto à área da circunferência

A .   c i r c = π r 2

unitária...

A .   c i r c = π ∙ 1 2 = π

Logo, podemos concluir que a área da região é

Á r e a   d e   R = A .   q u a d . - A . c i r c . =

8 - π

Passo 7

Voltando para Green, matamos a questão concluindo

∮ C   F d r + ∮ D   F d r = - Á r e a   d e   R

∮ C   F d r + ∮ D   F d r = - 8 - π = π - 8

Resposta

π - 8

Exercícios de Livros Relacionados

Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . x 2 y 2 d x + x y d y C consiste num arco de parábola y = x 2 indo de ( 0,0 ) para ( 1,1 ) e o
Utilize o Teorema de Green para demonstrar a fórmula de mudança de variáveis para as integrais duplas (Fórmula 15.9.9) para o caso onde f x , y = 1 : ∬ R d xd y = ∬ S ∂ x , y ∂ u , v d ud v Aqui, R é
Use o teorema de Green para calcular ∫ C F ⋅ d r . (Verifique a orientação da curva antes de aplicar o teorema.) F x , y = y 2 cos ⁡ x , x 2 + 2 y sen ⁡ x C é o triangulo de 0,0 �� ��a ( 2,6 ) a 2,0 a
Se C é o segmento de reta ligando o ponto ( x 1 , y 1 ) ao ponto ( x 2 , y 2 ) , mostre que ∫ C xd y - yd x = x 1 y 2 - x 2 y 1 Se os vértices de um polígono, na ordem anti-horária, são x 1 , y 1 ,x 2
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. ∫ C y + e x d x + 2 x + cos ⁡ y 2 d y C é a fronteira da região englobada pelas parábolas y = x