Determine o trabalho realizado pelo campo de força
Em uma partícula que se move da origem ao longo do eixo para , em seguida ao longo de um segmento de arco de circunferência até , e então de volta à origem ao longo do eixo .
Passo 1
Primeiro, vamos fazer um esboço da curva. Como o enunciado fala, temos um setor de circunferência de raio :
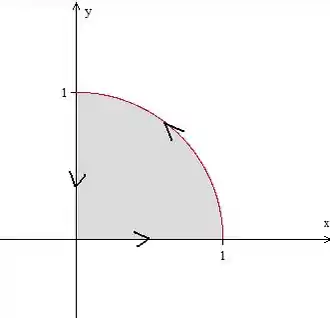
Cuidado com a orientação da curva, o enunciado fala que ela vai desde a origem até , depois, ao longo do arco, vai para e, em seguida, volta para a origem.
Bom, como parece ser meio trabalhoso calcular essa integral de linha pela definição (imagina substituir a parametrização da curva no campo), vamos tentar aplicar o Teorema de Green. A curva até já é fechada e orientada positivamente, para facilitar nossa vida!
Temos então
Passo 2
Beleza, agora precisamos calcular
Temos:
Como encontramos uma expressão relativamente simples, isso quer dizer que estamos no caminho certo!
Passo 3
Agora podemos montar a integral. Aplicando o teorema de Green, a integral do enunciado pode ser escrita como:
Onde é a região que vimos no passo .
Passo 4
Agora vamos ter que escrever matematicamente essa região. Bom, como temos um setor de circunferência e termos quadráticos na integral, o problema está implorando para a gente usar coordenadas polares, né? Olha só, vamos fazer:
Nossa região pode então ser escrita como e . Isso porque o raio varia desde a origem onde até a circunferência, onde e o ângulo faz de volta trigonométrica, ou seja, varia desde até .
Então, podemos reescrever a integral como
Passo 5
Beleza, agora é só resolver isso aí. Integrando em relação a :
Agora em relação a :