Use o Teorema de Green para calcular a área da região plana do primeiro quadrante delimitada por e .
Passo 1
A gente viu na teoria que podemos utilizar o teorema de Green para calcularmos a área de uma região se lembrarmos que a área pode ser calculada pela integral dupla:
E nós precisamos usar o Teorema de Green para calcular isso:
Então, podemos dizer que a integral de linha sobre a borda dessa região é igual a essa integral dupla sobre . Sendo , é claro, orientada no sentido anti-horário (positivo).
E a condição que temos que atender é, na verdade:
Então, tudo o que precisamos é de um campo que satisfaça essa condição. Vamos escolher um fácil né? Pode ser:
Nesse caso
Show! Agora podemos aplicar Green:
Logo, a área que queremos é dada pela integral de linha de em .
Passo 2
Vamos começar fazendo um esboço dessa região. Temos a reta (em vermelho) e a reta , que tem inclinação menor que a primeira (em azul). Temos também a curva (em verde):
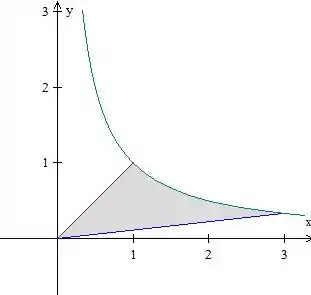
A região é essa aí em cinza.
Então, a fronteira dessa região, que vai ser nossa curva tem partes, não é? Vamos precisar calcular integrais de linha.
Vamos chamar de o segmento vermelho, de o azul e o verde. Isso nos dá:
Passo 3
Vamos, agora, parametrizar esses segmentos:
pertence à reta , portanto;
Para achar o ponto final devemos achar a interseção
Assim, .
pertence à reta , logo:
De novo, precisamos determinar a interseção
Ou seja, .
Já pertence a , o que nos dá:
Com variando de a .
Passo 4
Agora vamos derivar essas parametrizações:
Passo 5
Agora, vamos aplicar a fórmula:
Onde
Para :
Para :
Para :
Levando o que temos paras as integrais:
Passo 6
Agora é só resolver isso aí