Use o Teorema de Green para calcular
Onde é o triângulo com vértices , e , orientado no sentido anti-horário.
Passo 1
Ele diz para gente usar o teorema de Green para calcular uma integral de linha vetorial sobre o triângulo com vértices , e , orientado no sentido anti-horário. Vamos desenhar esse cara:
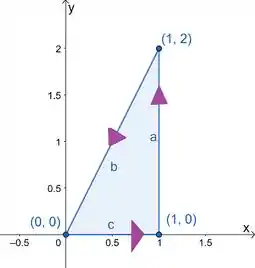
Então é esse caminho que a gente desenhou e no sentido das setinhas.
Passo 2
O Teorema de Green diz que a gente pode calcular a integral de em uma curva por essa relação:
Onde é uma região e é a curva fronteira dessa região. Só que ele tem umas condições para aplicar.
1. A nossa região precisa ser fechada: como a nossa região é limitada pelos lados do triângulo, ela tá fechada, belezinha.
2. A fronteira precisa ser percorrida no sentido positivo: Que sentido é esse? É só você imaginar que está andando na borda do triângulo no sentido das setinhas, sua região precisa está à sua esquerda. E isso acontece no nosso triângulo ali. Daora!
3. não pode ter descontinuidades dentro da nossa região. Aí a gente olha para o nosso :
Ela realmente está bem definida para todo . Não há nenhuma restrição no domínio. Então essa tá tranquilo também. Bora lá aplicar o Teorema!
Passo 3
Substituindo nele as coisas que a gente tem:
Bora calcular esse integrando ali:
Passo 4
Nossa integral fica assim:
A ideia é calcular o valor da integral de linha calculando essa integral dupla na direita. Sendo que é o nosso triângulo. Aí a gente precisa definir os extremos de integração para percorrer ele.
No eixo , vemos que ele está entre:
Já no eixo , ele é limitado por baixo por e por cima pela reta que passa por e . Achando a equação dessa reta:
Sendo
E escolhendo
Aí dizemos que:
Nossa integral fica:
Repara que a gente vai integrar em relação a primeiro porque ele está entre funções de .
Passo 5
Agora é calcular essa belezura:
Nessa integral de dentro o é considerado constante: