Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Green

Ver Teoria
Exercício 591234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575860616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFPE, Sem Campus, Cálculo 3, Listas de Exercícios de Cálculo 3 - Profº Cilon Perusato - Lista 3, Questão 2a

Questão 2. Use o Teorema de Green para calcular ∫ C F · d r . (Verifique a orientação da curva antes de aplicar o teorema.

(a) F x , y = y 2 cos ⁡ x ,   x 2 + 2 y sin ⁡ x , C é o triângulo de 0,0 para 2,6 , para 2,0 e para 0,0 ;

Passo 1

Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nesse problema queremos aplicar o teorema de Green para calcular a integral da função F x , y = y 2 cos ⁡ x ,   x 2 + 2 y sin ⁡ x em C , onde está é a região definida pelo triângulo cujos vértices seguem os pontos 0,0 , 2,6 , 2,0 e volta para 0,0 .

E aí, lembra como fazemos isso? 😁

Fazendo ∫ C F · d r onde F é uma função genérica dada por F x , y = p x , y , q x , y , temor

∫ C F · d r = ∫ C p x , y , q x , y · d x , d y

∫ C F · d r = ∫ C p x , y d x + q x , y d y

O teorema de Green é dado por

∫ C F · d r = ∫ C p x , y d x + q x , y d y = ∫ ∫ A ∂ q ∂ x - ∂ p ∂ y d A

Onde A é a área da curva C fechada.

Sacou? Bora lá! 😉

Passo 2

No nosso caso, p x , y = y 2 cos ⁡ x e q x , y = x 2 + 2 y sin ⁡ x ...

Derivando q em relação a x e p em relação a y , vamos obter

∂ q ∂ x = ∂ x 2 + 2 y sin ⁡ x ∂ x = 2 x + 2 y cos ⁡ x

∂ p ∂ y = ∂ y 2 cos ⁡ x ∂ y = 2 y cos ⁡ y

Aplicando o teorema de Green, temos

∫ C F · d r = ∫ C p x , y d x + q x , y d y = ∫ ∫ A 2 x + 2 y cos ⁡ x - 2 y cos ⁡ y d A

∫ C F · d r = ∫ ∫ A 2 x d A

Agora temos que definir a região de integração em uma integral dupla...

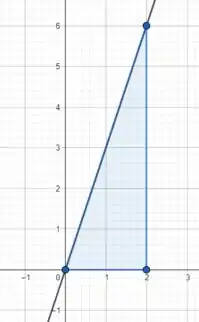
Esboçando os vértices dados, temos

Tranquilo até aqui? 😎

Passo 3

Alongando a linha que passa por 0,0 e 2,6 podemos definir uma reta como

y = m x + a

Como essa reta corta o eixo y em y = 0 , então a = 0 também.

Já m pode ser obtido como a razão de subida... quando x = 2 , y = 6 (três vezes maior) então a razão de subida é dada por m = 3 .

y = 3 x

Assim, podemos afirmar que y varia de 0 a 3 x e x varia de 0 a 2 .

Assim, nossa região de integração é dada por

∫ C F · d r = ∫ 0 2 ∫ 0 3 x 2 x d y d x

Como não há y para integrar, multiplicamos a função de integração pela diferença dos limites de integração e passamos para a próxima integral

∫ C F · d r = ∫ 0 2 2 x 3 x - 0 d x = ∫ 0 2 6 x 2 d x

Integrando com relação a x ...

∫ 6 x 2 d x = 2 x 3

∫ 0 2 6 x 2 d x = 2 2 3 - 0 = 16

Portanto, encontramos que

∫ C F · d r = 16

Fim! Iae, o que achou? Responde Aí! 😁

Resposta

∫ C F · d r = 16

Exercícios de Livros Relacionados

Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . x 2 y 2 d x + x y d y C consiste num arco de parábola y = x 2 indo de ( 0,0 ) para ( 1,1 ) e o
Utilize o Teorema de Green para demonstrar a fórmula de mudança de variáveis para as integrais duplas (Fórmula 15.9.9) para o caso onde f x , y = 1 : ∬ R d xd y = ∬ S ∂ x , y ∂ u , v d ud v Aqui, R é
Use o teorema de Green para calcular ∫ C F ⋅ d r . (Verifique a orientação da curva antes de aplicar o teorema.) F x , y = y 2 cos ⁡ x , x 2 + 2 y sen ⁡ x C é o triangulo de 0,0 �� ��a ( 2,6 ) a 2,0 a
Se C é o segmento de reta ligando o ponto ( x 1 , y 1 ) ao ponto ( x 2 , y 2 ) , mostre que ∫ C xd y - yd x = x 1 y 2 - x 2 y 1 Se os vértices de um polígono, na ordem anti-horária, são x 1 , y 1 ,x 2
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. ∫ C y + e x d x + 2 x + cos ⁡ y 2 d y C é a fronteira da região englobada pelas parábolas y = x