Calcule as seguintes integrais de linha:
Onde é o triângulo de vértices , , , percorrido no sentido anti-horário.
Passo 1
Bem, a expressão desse campo é bem simples, então podemos calcular essa integral pela definição sem problemas. Acontece que, como temos três segmentos de reta, temos que fazer três parametrizações e resolver três integrais de linha... então de repente vale à pena usar Green, né? Temos isso aqui:
Passo 2
Agora vamos dar uma olhada nessa curva . Temos isso aqui:
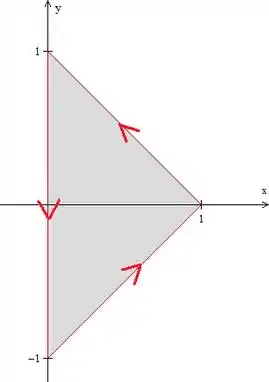
Beleza, como a curva está orientada positivamente e o campo está definido dentro dela, podemos escrever o seguinte:
Ou seja:
Passo 3
Agora vamos escrever essa região como tipo I e resolver essa integral.
Para isso, precisamos das equações das reta inclinadas. A de cima, liga os pontos e , substituindo na equação geral da reta, temos:
Para a reta debaixo, temos os pontos e :
Como varia entre a reta inclinada debaixo e a de cima, temos . E , como podemos ver, varia de a . Levando para a integral:
Passo 4
Agora é só resolver isso aí: