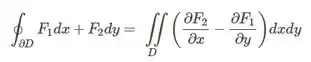Seja .
- Use o Teorema de Green para calcular
onde é a fronteira da região englobada pelas parábolas e
Passo 1
Bom, Green nos diz que:
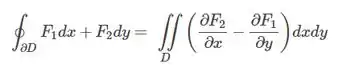
Com isso ficamos com
Passo 2
Agora falta a gente identificar nossa região pra poder escrever!
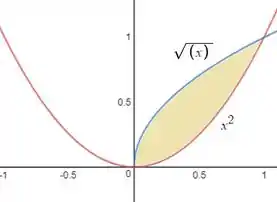
Pra identificarmos o porto de encontro das funções, basta a gente igualar as funções trabalhadas. Então vamo lá:
Logo
Beleza, então agora podemos ver que nosso x varia de 0 a 1, e o y entre a função de baixo () e a de cima .
Passo 3
Show, então agora a gente consegue escrever nossa integral.
Resposta
Exercícios de Livros Relacionados
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . x 2 y 2 d x + x y d y C consiste num arco de parábola y = x 2 indo de ( 0,0 ) para ( 1,1 ) e o
Utilize o Teorema de Green para demonstrar a fórmula de mudança de variáveis para as integrais duplas (Fórmula 15.9.9) para o caso onde f x , y = 1 : ∬ R d xd y = ∬ S ∂ x , y ∂ u , v d ud v Aqui, R é
Use o teorema de Green para calcular ∫ C F ⋅ d r . (Verifique a orientação da curva antes de aplicar o teorema.) F x , y = y 2 cos x , x 2 + 2 y sen x C é o triangulo de 0,0 �� ��a ( 2,6 ) a 2,0 a
Se C é o segmento de reta ligando o ponto ( x 1 , y 1 ) ao ponto ( x 2 , y 2 ) , mostre que ∫ C xd y - yd x = x 1 y 2 - x 2 y 1 Se os vértices de um polígono, na ordem anti-horária, são x 1 , y 1 ,x 2
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. ∫ C y + e x d x + 2 x + cos y 2 d y C é a fronteira da região englobada pelas parábolas y = x