Considere a curva plana orientada definida pela parametrização
Seguida do segmento de a e do segmento de a . Calcule a integral de linha
Passo 1
Bom, olhando para a expressão desse campo, parece um pouco complicado calcular essa integral de linha pela definição, deve dar trabalho. Vamos tentar usar Green então;
Precisamos, antes de tudo, calcular
Temos:
Como encontramos uma expressão simples, isso quer dizer que estamos no caminho certo!
Passo 2
O enunciado já nos deu uma curva fechada, então, só precisamos verificar sua orientação para aplicar Green.
Sabemos que é uma elipse parametrizada, como o enunciado fala que vai de até , temos um setor de elipse. Calma que não é tão simples, pois temos não c. Em , temos o ponto e em , o ponto . Juntando esse arco com os segmentos de até e de até , temos:
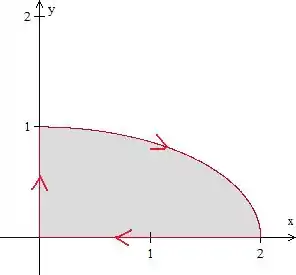
Porém, para aplicar Green, a curva deve estar no sentido anti-horário. Assim, podemos escrever o seguinte:
Onde é a curva com orientação oposta:
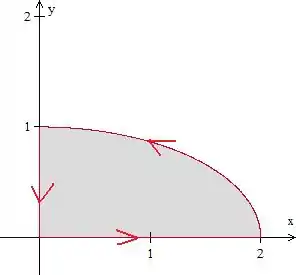
Como queremos a integral de linha em :
Passo 3
Agora podemos montar a integral. Aplicando o teorema de Green, a integral do enunciado pode ser escrita como:
Onde é a região que vimos no passo anterior.
Passo 4
Agora vamos resolver essa integral. Mas nem precisa, né? Olha só:
Como nós sabemos que a área de uma elipse é dada por:
E, pela parametrização
Temos que e , temos:
Como é da elipse: