Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Green

Ver Teoria
Exercício 401234567891011121314151617181920212223242526272829303132333435363738394142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Integral de linha – caso vetorial, Teorema de Green

Considere o caminho C que delimita a região do plano limitada pelas linhas de equação y = x 2 e x = y 2 e percorrido no sentido anti-horário.

  1. Usando a definição, calcule a integral de linha

    2. ∫ C x 2 y d x + y + x y 2 d y

    (não precisa resolver a integral)

  2. Calcule a integral do item a , agora usando o teorema de Green

Passo 1

A primeira coisa que temos que fazer aqui é entender como é essa limitação da região. Para isso vamos ver onde as duas equações se cruzam

y = x 2

x = y 2

Substituindo o valor de x da segunda equação na primeira vamos ter

y = y 2 2

y = y 4

y 4 - y = 0

y y 3 - 1 = 0

y = 0         o u         y 3 - 1 = 0

y = 0         o u         y 3 = 1

y = 0         o u         y = 1

Então as equações vão se cortar em y = 0 e y = 1 , os pontos vão ser

y = 0 ⇒ x = 0 2 = 0

y = 1 ⇒ x = 1 1 = 1

Então eles se cortam nos pontos 0,0 e 1,1 . Vamos ver como fica o gráfico disso

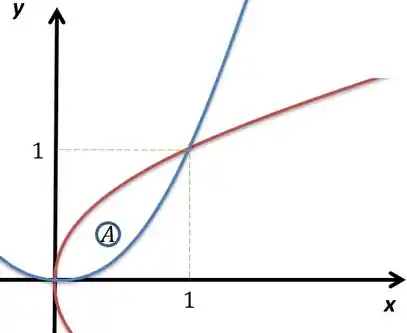
A curva azul é y = x 2 e a curva vermelha é x = y 2 .

Como ele quer no sentido anti-horário devemos seguir por C 1 e - C 2 onde C 1 é a curva azul indo de 0,0 até 1,1 e C 2 é a curva vermelha indo de 0,0 até 1,1 , colocamos o – para mudar o sentido de C 2 e rodar tudo no sentido anti-horário.

Vamos ter

∫ C x 2 y d x + y + x y 2 d y = ∫ C 1 x 2 y d x + y + x y 2 d y - ∫ C 2 x 2 y d x + y + x y 2 d y

A outra coisa que precisamos perceber é que a integral de linha é da função F

F x , y = x 2 y , y + x y 2

Passo 2

Vamos começar com C 1 , primeiro precisamos parametrizar a curva C 1

Vamos fazer

x = t

y = t 2

C 1 t = t , t 2

Com

t ∈ 0,1

Derivando isso vamos ter

C 1 ' t = 1,2 t

A integral vai ficar

∫ C 1 x 2 y d x + y + x y 2 d y = ∫ C 1 F C 1 t ∙ C 1 ' t d t = ∫ 0 1 t 2 t 2 , t 2 + t . t 2 2 ∙ 1,2 t d t

⇒ ∫ 0 1 t 4 , t 2 + t . t 4 ∙ 1,2 t d t = ∫ 0 1 t 4 , t 2 + t 5 ∙ 1,2 t d t = ∫ 0 1 t 4 + 2 t 3 + 2 t 6 d t

Ele disse para não calcular a integral, então vamos deixar assim.

Passo 3

Vamos fazer agora aquela integral de C 2 , primeiro precisamos parametrizar a curva C 2

Vamos fazer

x = t 2

y = t

C 2 t = t 2 , t

Com

t ∈ 0,1

Derivando isso vamos ter

C 2 ' t = 2 t , 1

A integral vai ficar

∫ C 1 x 2 y d x + y + x y 2 d y = ∫ C 1 F C 2 t ∙ C 2 ' t d t = ∫ 0 1 t 2 2 t , t + t 2 . t 2 ∙ 2 t , 1 d t

⇒ ∫ 0 1 t 4 t , t + t 4 ∙ 2 t , 1 d t = ∫ 0 1 t 5 , t + t 4 ∙ 2 t , 1 d t = ∫ 0 1 2 t 6 + t + t 4 d t

Ele disse para não calcular a integral, então vamos deixar assim.

Passo 4

A nossa integral de linha vai ficar

∫ C x 2 y d x + y + x y 2 d y = ∫ 0 1 t 4 + 2 t 3 + 2 t 6 d t - ∫ 0 1 2 t 6 + t + t 4 d t

Como os limites de integração são iguais podemos juntar essas integrais

∫ 0 1 t 4 + 2 t 3 + 2 t 6 - 2 t 6 + t + t 4 d t = ∫ 0 1 t 4 + 2 t 3 + 2 t 6 - 2 t 6 - t - t 4 d t = ∫ 0 1 2 t 3 - t d t

E essa é a integral que teríamos que fazer, mas ele não quer que faça quer que deixe indicado só.

Passo 5

b )

Como a função F é contínua nessa região A podemos fazer aplicar o teorema de Green.

∫ C x 2 y d x + y + x y 2 d y = ∬ A ∂ F 2 ∂ x - ∂ F 1 ∂ y d A

Vamos achar aquele termo ali dentro, lembrando que

F 2 = y + x y 2

F 1 = x 2 y

Vamos as derivadas

∂ F 2 ∂ x = y 2

E

∂ F 1 ∂ y = x 2

A integral dupla vai ficar

∬ A y 2 - x 2 d A

Vamos entender como é a região A , já vimos o seu gráfico

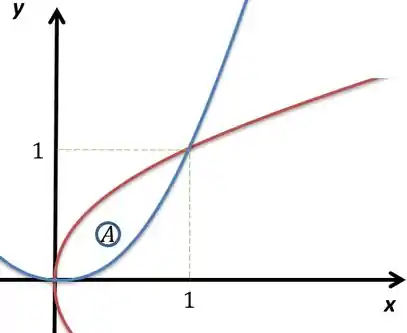
Repara que vamos ter x indo de 0 à 1 enquanto y vai da função azul até a função vermelha.

Vamos ver como são essas duas funções em y

Função azul

y = x 2

A função vermelha

x = y 2

y = x

A região A vai ser

A = x , y ∈ R 2 0 ≤ x ≤ 1 , x 2 ≤ y ≤ x

Passo 6

A integral vai ficar

∬ A y 2 - x 2 d A = ∫ 0 1 ∫ x 2 x y 2 - x 2 d y d x

Vamos à integral

∫ 0 1 ∫ x 2 x y 2 - x 2 d y d x = ∫ 0 1 y 3 3 - x 2 y y = x 2 x d x

⇒ ∫ 0 1 x 3 3 - x 2 x - x 2 3 3 - x 2 x 2 d x

⇒ ∫ 0 1 x 1 / 2 3 3 - x 2 x 1 / 2 - x 6 3 - x 4 d x

⇒ ∫ 0 1 x 3 / 2 3 - x 2 + 1 / 2 - x 6 3 - x 4 d x

⇒ ∫ 0 1 x 3 / 2 3 - x 5 / 2 - x 6 3 - x 4 d x

⇒ ∫ 0 1 x 3 / 2 3 - x 5 / 2 - x 6 3 + x 4 d x

⇒ x 5 / 2 3 5 / 2 - x 7 / 2 7 / 2 - x 7 3 7 + x 5 5 x = 0 x = 1

⇒ x 5 / 2 3 2 5   - 2 7 x 7 / 2 - x 7 21 + x 5 5 x = 0 x = 1

⇒ 2 x 5 / 2 15   - 2 7 x 7 / 2 - x 7 21 + x 5 5 x = 0 x = 1

⇒ 2 . 1 5 / 2 15   - 2 7 1 7 / 2 - 1 7 21 + 1 5 5 - 2 . 0 5 / 2 15   - 2 7 0 7 / 2 - 0 7 21 + 0 5 5

⇒ 2 15   - 2 7 - 1 21 + 1 5 - 0

⇒ 2 15   - 2 7 - 1 21 + 1 5

⇒ 14 - 30 - 5 + 21 105 = 35 - 35 105 = 0

Resposta

  1. ∫ 0 1 2 t 3 - t d t
  2. 0

Exercícios de Livros Relacionados

Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . x 2 y 2 d x + x y d y C consiste num arco de parábola y = x 2 indo de ( 0,0 ) para ( 1,1 ) e o
Utilize o Teorema de Green para demonstrar a fórmula de mudança de variáveis para as integrais duplas (Fórmula 15.9.9) para o caso onde f x , y = 1 : ∬ R d xd y = ∬ S ∂ x , y ∂ u , v d ud v Aqui, R é
Use o teorema de Green para calcular ∫ C F ⋅ d r . (Verifique a orientação da curva antes de aplicar o teorema.) F x , y = y 2 cos ⁡ x , x 2 + 2 y sen ⁡ x C é o triangulo de 0,0 �� ��a ( 2,6 ) a 2,0 a
Se C é o segmento de reta ligando o ponto ( x 1 , y 1 ) ao ponto ( x 2 , y 2 ) , mostre que ∫ C xd y - yd x = x 1 y 2 - x 2 y 1 Se os vértices de um polígono, na ordem anti-horária, são x 1 , y 1 ,x 2
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. ∫ C y + e x d x + 2 x + cos ⁡ y 2 d y C é a fronteira da região englobada pelas parábolas y = x