Use o teorema de Green para calcular a integral de linha dada por
Onde é a curva de orientação positiva dada pela fronteira da região delimitada pelas parábolas e .
Passo 1
O enunciado fala pra gente usar o teorema de Green aqui, lembra o que esse teorema fala?
Onde a região tem como fronteira a curva fechada orientada positivamente.
Pra aplicar isso na questão, vamos entender como é o nosso esboço! Temos duas parábolas aqui, assim:
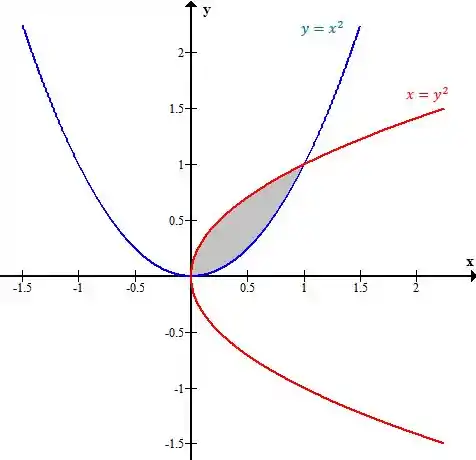
Então é nessa região mesmo que vamos aplicar o teorema! Veja que transformamos uma integral de linha difícil em uma integral dupla mais simples, beleza?
Precisamos então calcular esse termo e encontrar os limites da região de integração, vamos lá?
Passo 2
Começando pelo termo dentro da integral dupla
Onde
Derivando isso aí
Passo 3
Vamos encontrar os limites agora. Analisando o esboço, tanto faz uma região do tipo ou do tipo , é tudo simétrico aqui. Vamos fazer pelo tipo então, precisamos
Olhando a região , a curva precisa ser escrita de outra forma
Vamos pegar a raiz positiva só mesmo porque é a que está no esboço. Olha só como fica
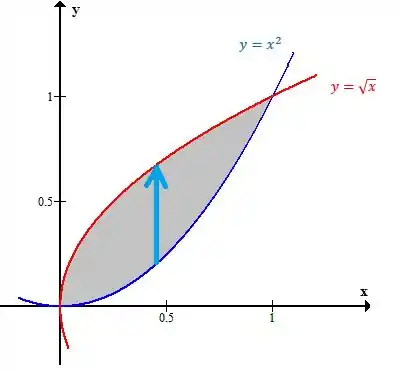
Portanto os limites de são
Os limites de são as interseções das curvas, ou seja, nos pontos e
Passo 4
Definido isso, agora é só botar tudo na integral
Passo 5
Vamos resolver a integral aqui
Integrando em