Seja a região delimitada pelas curvas
E
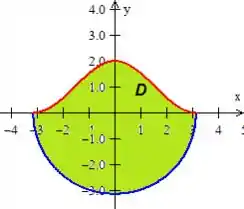
- Faça um esboço da região .
- Seja
e seja a união de e , orientada negativamente. Calcule
Passo 1
Letra a) Bem, antes de desenhar a região propriamente dita, que tal olharmos para cara duma dessas curvas aí primeiro?:)
A primeira delas, bem típica, é uma circunferência de um raio peculiar: .
Mas calma! Não é toda circunferência! É só a parte de baixo dela que queremos, pois
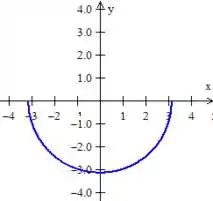
Quanto à outra curva, ela é o cosseno,
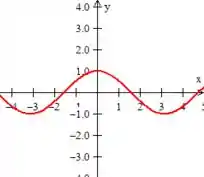
Mas não é bem esse cosseno, pois além dele estar limitado de até , ela está deslocada uma unidade pra cima em
Unindo as duas curvas, vamos obter a curva fechada , delimitando a região
Passo 2
Letra b) Hum! Região fechada...! Campo vetorial estranho...! Sei não, heim! tá sugerindo Green .
Para ter certeza, vamos calcular o rotacional desse campo:
Onde essa e aí são
Ou seja, é a primeira componente e a é a segunda.
Então bora calcular essas derivadas aí e verificar se aquele rotacional vai ser simples?
Passo 3
Primeiro vamos calcular a primeira derivada :
Aplicando a regra da soma...
As duas últimas derivadas morrem fáceis, pois tomando como constante
Ficando então para derivarmos parcialmente essa fração aí, então vamos com calma aqui:
Aplicando a regra do quociente...
Calma! Não se assuste. Isso vai simplificar agora calculando essas derivadas parciais no denominador
Começou a simplificar...
Não disse?
Então
Passo 4
Fazendo o mesmo, porém agora para aquela outra derivada parcial que precisamos
A segunda derivada morre, ficando só a primeira:
Fazendo como acima, ou seja, aplicando a regra do quociente para essa outra derivada
Derivando
Ou seja
Passo 5
Se a gente voltar para o rotacional e jogar lá naquela fórmula o que a gente já obteve
Veja só, vamos cortar esses caras cabulosos :D
Ou seja, o rotacional realmente simplifica a nossa vida. Como o campo não tem singularidade dentro da nossa região (ele tem uma singularidade fora que não nos interessa ;D), poderemos aplicar Green:
Onde esse é a borda da região orientada positivamente, ou seja, é , mas com o sinal trocado (o problema disse que estava orientada negativamente)
Bele? Então bora calcular essa integral dupla aí e matar o problema!
Passo 6
Substituindo o rotacional que a gente calculou
Agora, quem é a integral de ? É a área da região ! :D
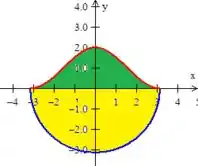
Como essa região é a união desse semicírculo de raio amarelo, com a área verde, temos
Onde
Para a área verde, não conhecemos uma função já pronta como a do círculo, então...
Passo 7
Vamos resolvê-la utilizando a integral dupla mesmo:
Primeiro devemos descrever essa região verde, que podemos descrever como uma região do tipo 1, ou seja
- varia de
- varia desde até a função azul
Montando a integral
Integrando em
Substituindo os limites
Integrando...
Substituindo os limites
Passo 8
Retornando ondo paramos...
Resposta
Letra a)
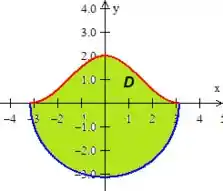
Letra b)