UFSC – Cálculo 1 – Lista 1.9 – Assíntotas – 21.1 – P1 – letra (g)
Para cada uma das funções abaixo, determine as assíntotas horizontais e verticais.
Passo 1
Primeiro passo é a gente entender como calculamos uma assíntota vertical e uma horizontal.
De forma bem sucinta e prática:
Assíntota horizontal: Fazemos e e se , onde c é uma constante, temos uma assíntota horizontal. Lembrando que podemos ter valores de constantes dependendo se estamos fazendo e , logo teríamos 2 assíntotas horizontais nesses dois valores diferentes de constantes.
Assíntota vertical: Precisamos encontrar um valor de que faça o denominador tender a zero, se a , temos então uma assíntota vertical no valor que fizemos tender.
Então, bora pro rolo!
Passo 2
Pra gente encontrar a assíntota horizontal, vamos aplicar nosso limite!
Opa, temos assíntota horizontal em
Passo 3
Analisando a assíntota vertical: Note que se a gente fizer lá do exponencial tender a infinito, então . Note que isso pode ser feito se fizermos e, por consequência, teremos a segunda parcela da soma de tendendo a infinito.
Logo, temos assíntota vertical em
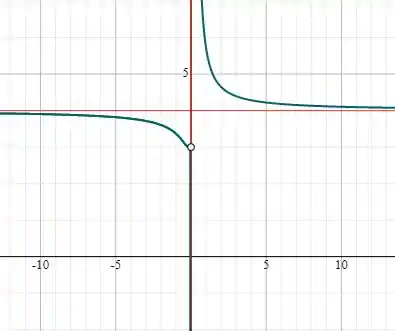
Resposta
Assíntota horizontal:
Assíntota vertical: