UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Profº Edson Figueiredo - 2ª Lista, Questão 7
Nos exercícios 05 a 12, calcule o volume do sólido descrito em cada caso, usando integração tripla.
Sólido interior ao cilindro , sendo delimitado pela esfera e pelo plano .
Passo 1
Olá meu amigo, Yuri aqui e agora iremos calcular o volume do sólido dado. Iremos utilizar aqui a integração tripla, e antes de tudo vamos dar uma olhada no nosso solido.
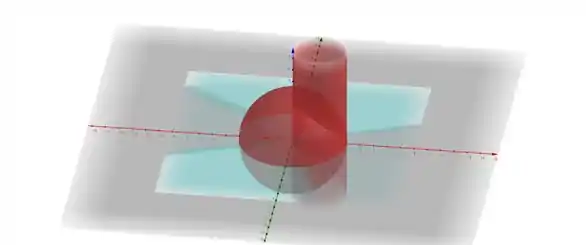
Basicamente o que acontece é que superiormente estamos limitados pela esfera, inferiormente pelo plano e lateralmente pelo cilindro.
Passo 2
A equação do cilindro deslocado pode também ser dado por
Para facilitar a minha vida e a sua, iremos trabalhar com coordenadas polares:
O ângulo é o ângulo que varre a região do cilindro deslocado,
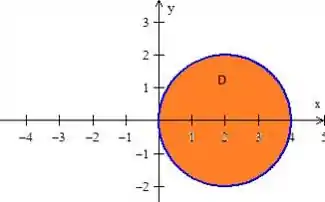
Então . O Nosso raio é dado por
Agora falta parametrizar a esfera
E como somo limitados pelo plano
Passo 3
Calculando nossa integral
Chamando de e e os limites novos, e
Simplificando
Continuando
Como a função seno é impar, a primeira integral é zero, então