UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Profº Edson Figueiredo - 2ª Lista, Questão 10
Nos exercícios 05 a 12, calcule o volume do sólido descrito em cada caso, usando integração tripla.
Sólido continho no coze , limitado pela esfera .
Passo 1
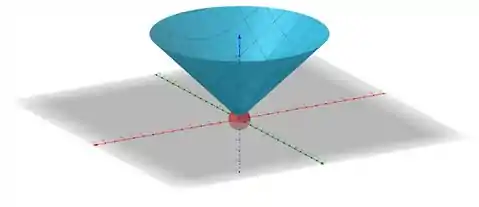
Para calcular o volume do sólido com a imagem acima, que está contido na região delimitada pela superfície e pela esfera , podemos usar integração tripla. Vamos usar coordenadas esféricas para simplificar o cálculo, já que a região de integração possui simetria esférica.
As coordenadas esféricas são definidas da seguinte forma:
1. é a distância do ponto à origem, ou seja, .
2. é o ângulo polar, que varia de 0 a .
3. é o ângulo azimutal, que varia de 0 a .
Vamos escrever as equações de conversão entre coordenadas cartesianas e coordenadas esféricas :
Passo 2
Agora, precisamos encontrar os limites de integração para , , e . Primeiro, vamos lidar com . Sabemos que a esfera tem raio 1, então varia de 0 a 1.
Para , podemos ver que a superfície se estende de a o que define o ponto de interseção entre a superfície e a esfera). Portanto, os limites de integração para são de 0 a .
Para , como não há restrições quanto a , ele varia de 0 a .
Agora, podemos escrever a integral tripla para calcular o volume:
Agora, podemos calcular essa integral: