USP, São Carlos, Calculo 2, Listas de C2 - Grupo Coordenado 2022 - Lista 3 - Módulo 3, Questão 10b
10. Descreva a superfície de nível para :
(b)
Passo 1
Iae! Como vai, meu querido? 😁 Bora aprender mais uma questão? 😉
Nesse problema queremos as curvas de nível da função nos níveis .
Lembra como fazemos isso? 🤔
O que temos que fazer é igualar a função a uma variavel que representa o nível da função que temos que representar...
Assim temos que atribuir a os valores e em cada equação formada, vamos ter um gráfico tridimensional que vamos ter que representar no espaço cartesiano.
Sacou? Bora ver como é na prática! 😉
Passo 2
Igualando a função a , temos
Elevando os dois lados ao quadrado, vamos obter
Perceba que a equação obtida é exatamente igual a equação da esfera centrada na origem com sendo o raio da esfera...
Por exemplo, para
Para
Para
Esboçando essas esferas no espaço, temos
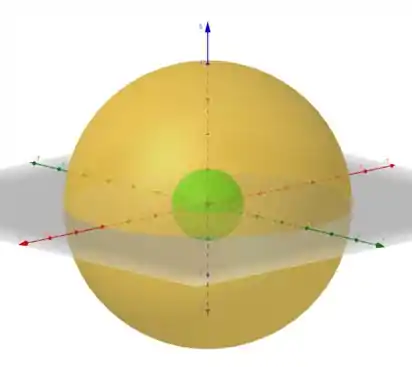
Pegou o esquema? Responde Aí! 😁
Resposta
