UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 4.
4 - Calcule , onde é a região delimitada por e .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nessa questão, temos uma função e temos que calcular a sua integral dupla na região , sendo limitada pelas curvas e .
E aí! Como vamos determinar nossos limites de integração? 🤔
Primeiro de tudo, vamos ver como é as curvas formadas pela região ?
Plotando as curvas e , temos
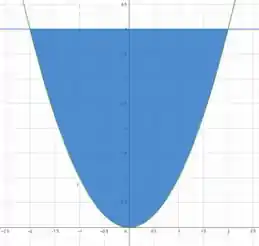
Assim, conseguimos visualizar a região de integração.
Passo 2
Babemos que o limite superior é dado pela maior curva, ou seja, em , os limites de integração vão de a .
Se e , , logo, os limites de integração em vai de a .
Com isso, nossa integral é formada por
Mas se você encontrou
Relaxa, o resultado será o mesmo, apenas as integrais estão invertidas.
Vamos resolver a primeira integral.
Integrando com relação a , pelo método de integração polinomial (dividindo a variável pela potência e somando no expoente) e lembrando que agora e se comportam como constantes.
Aplicando os limites de integração
Tranquilo até aqui? 👀
Passo 3
Agora com esse resultado, vamos integrar com relação a pelo mesmo método de integração polinomial.
Como agora temos um polinômio mais longo, vamos integrar separadamente e junta-los no fim.
Juntando tudo no mesmo resultado, temos
Agora temos que aplicar os limites de integração.
Para o limite superior , temos
Para o limite inferior , temos
Subtraindo o resultado do limite superior e o resultado do limite inferior, temos
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
