Uma camada esférica condutora neutra tem raio interno e raio externo . No centro da camada, na cavidade interna, há uma carga puntiforme .
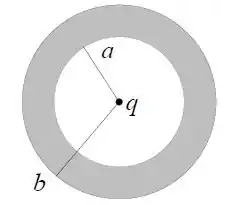
- Usando a lei de Gauss e propriedades dos condutores em equilíbrio eletrostático determine as densidades superficiais de carga e nas superfícies interna e externa da camada esférica.
- Calcule o vetor campo elétrico em todo o espaço.
Passo 1
- Usando a lei de Gauss e propriedades dos condutores em equilíbrio eletrostático determine as densidades superficiais de carga e nas superfícies interna e externa da camada esférica.
- Calcule o vetor campo elétrico em todo o espaço.
Vamos lá! Sabemos que, no equilíbrio eletrostático, não existe movimento de cargas no interior do condutor e, mais importante do que isso... o campo elétrico no interior de um condutor é igual a zero. Se não sabia, agora sabe!
Sabendo que o campo elétrico é nulo do interior de um condutor, basta aplicar a lei de Gauss.
A lei de Gauss fala o seguinte!
Nesse caso, vamos escolher para gaussiana a esfera de raio , sendo . Mais ou menos com essa cara aqui:
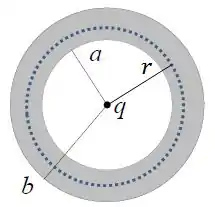
Passo 2
Na gaussiana escolhida, a carga interna é dada por:
Onde é a carga na superfície interna da camada esférica.
Substituindo na lei de Gauss.
A densidade superficial de carga na superfície interna é dada por:
Passo 3
A camada esférica é originalmente eletricamente neutra.
Quando colocamos a carga no interior dessa camada, essa carga induz as cargas no condutor.
O resultado disso é que a carga fica localizada na superfície interna da camada. Mas como a carga no condutor deve ser neutra, a carga na superfície externa é dada por:
Portanto, a densidade superficial de carga na superfície externa é dada por:
Passo 4
Bom, analisando a situação, só temos três casos possíveis, então vamos analisar cada um deles a partir da lei d Gauss:
- :
- :
- :
Passo 5
Nesse caso, a carga interna é nula, como já vimos antes. Logo:
Passo 6
Sabendo que a carga interna , de acordo com a lei de Gauss: