Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Gauss – Simetrias

Ver Teoria
Exercício 122123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

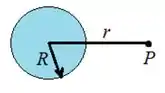
Uma carga elétrica está uniformemente distribuída dentro de uma esfera isolante de raio

0,30   m . O campo elétrico num ponto P , que se encontra a 0,60   m do centro da esfera é de 1,5 × 10 4   N / C apontando radialmente para fora da esfera. Qual o valor máximo do campo elétrico gerado por esta esfera?

  1. 9 × 10 4   N / C
  2. 6 × 10 4   N / C
  3. 4 × 10 4   N / C
  4. 3 × 10 4   N / C
  5. 2 × 10 4   N / C

Passo 1

Como a carga está uniformemente distribuída dentro da esfera, temos que a densidade de carga é dada por

ρ = q 4 3 π R 3

Em uma esfera de raio r < R concêntrica à esfera carregada, a carga total é dada por

q i n t = ρ V = q 4 3 π R 3 4 3 π r 3

q i n t = q r 3 R 3

Pela lei de Gauss temos

∫ E → . d A → = q i n t ϵ 0

4 π r 2 E = q ϵ 0 r 3 R 3

E = q 4 π ϵ 0 r R 3 ,   ( r < R )

Já para uma gaussiana de raio r ≥ R , temos que a carga total dentro da gaussiana é a carga total da esfera

E = q 4 π ϵ 0 1 r 2 ,   ( r ≥ R )

Analisando o campo elétrico nas duas regiões vemos que ele é máximo para r = R .

Passo 2

O ponto P está a uma distância r = 2 R = 0,6 m , ou seja

E P = q 4 π ϵ 0 1 2 R 2 = 1,5 × 10 4 N / C

Já o campo em r = R seria

E r = R = q 4 π ϵ 0 1 R 2

Olhando de novo para o campo em P podemos reescrever

E P = q 4 π ϵ 0 1 2 R 2 = 1 4 q 4 π ϵ 0 1 R 2 = 1 4 E r = R

Assim

E r = R = 4 E P = 4 × 1,5 × 10 4

E r = R = 6 × 10 4 N / C

Resposta

(B)

Exercícios de Livros Relacionados

A Fig. 23-30 mostra uma superfície gaussiana com a forma de um cubo de 2,00 m de aresta, imersa em um campo elétrico dado porE → = 3,00 x + 4,00 i ^ + 6,00 j ^ + 7,00 k ^ N / C , com x em metros. Qual
Uma fina casca esférica não-condutora de raio R 1 tem carga total q 1 uniformemente distribuída em sua superfície. Uma segunda fina casca esférica não condutora e maior, de raio R 2 , coaxial com a pr
Uma esfera de raio R tem densidade volumétrica de carga ρ = B / r para rR , onde B é uma constante e ρ = 0 para rR . (a) Determine a carga total na esfera. (b) Determine as expressões par ao campo elé
Um cilindro sólido não condutor infinitamente longo de raio a tem uma massa específica volumétrico uniforme de ρ 0 . Mostre que o campo elétrico é dado pelas seguintes expressões: E R = ρ R / 2 ε 0 pa
Uma fina casca cilíndrica de comprimento 200m e raio 6,00c m tem uma densidade superificial uniforme de carga de 9,00n C / m 2 . (a) Qual é a carga total na casca? Determine o campo elétrico nas segui