Uma carga positiva é distribuída uniformemente pelo volume de cada uma de duas esferas isolantes de raio . Como mostra a figura, uma das esferas está centrada na origem e a outra está centrada em .
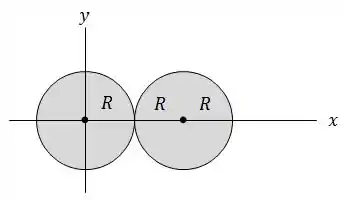
Encontre o vetor campo elétrico resultante devido a essas esferas nos seguintes pontos:
de coordenadas ;
de coordenadas ;
de coordenadas ;
Passo 1
de coordenadas ;
Para qualquer ponto, o campo elétrico será a soma vetorial dos campos elétricos gerados por cada esfera, da esquerda e da direita.
Devido à simetria esférica, o campo elétrico gerado por uma esfera carregada tem direção radial.
O ponto encontra-se no centro da esfera da esquerda, logo, em :
O campo elétrico gerado pela esfera da direita é determinado através da lei de Gauss, que é dada por:
Como o ponto está a uma distância do centro da esfera da direita, a nossa gaussiana aqui será uma esfera de raio , que engloba toda a esfera da direita.
Logo:
E podemos simplificar a lei de Gauss para:
Como concluímos anteriormente, tem direção radial, logo, em :
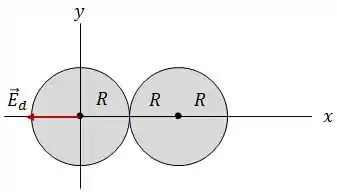
Finalmente:
Passo 2
de coordenadas ;
O ponto encontra-se dentro da esfera da esquerda. Como se trata de uma esfera isolante, o campo elétrico gerado pela esfera da esquerda no ponto será diferente de zero.
Tudo o que falamos antes sobre a simetria do problema, continua valendo aqui. Então, novamente, vamos usar a lei de Gauss para determinar o campo elétrico gerado pela esfera da esquerda.
Aqui, a gaussiana pra será uma esfera de raio , que envolve apenas parte da esfera da esquerda, logo:
Como se trata de uma esfera isolante, para determinar a carga interna, vamos usar uma regra de três, associando os volumes com as cargas.
Finalmente:
Como tem direção radial:
Passo 3
Para a esfera da direita também vamos usar a lei de Gauss:
Como o ponto está a uma distância de do centro da esfera da direita, a nossa gaussiana aqui será uma esfera de raio , que envolve toda a esfera da direita, logo:
Logo, em :
Sendo assim:
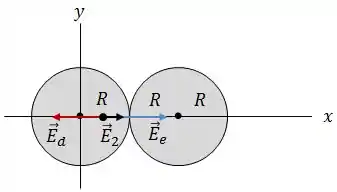
Passo 4
de coordenadas ;
O ponto está localizado na parte de cima da esfera da esquerda.
Para a esfera da esquerda, a gaussiana será uma esfera de raio , que engloba toda a esfera de carga , logo:
Como está localizado na parte de cima da esfera da esquerda:
Para a esfera da direita, a gaussiana será uma esfera cujo raio é a distância do centro da esfera da direita ao ponto , que será dado por:
Logo:
Pra determinar , antes, vamos dar uma olhada na situação:
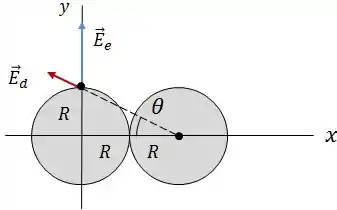
Daqui podemos tirar que:
Onde:
Logo:
Finalmente:
Resposta