Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Gauss – Simetrias

Ver Teoria
Exercício 109123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Densidade de Carga, Lei de Gauss, Campo em Condutores

Uma carga puntiforme - 3 Q está no centro C de uma camada esférica condutora de raio interno a e raio externo b , carregada com uma carga + 5 Q .

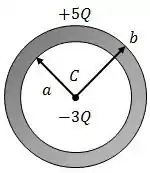
a ) Utilizando a Lei de Gauss, determine o campo elétrico E → r , para r < a ,   a < r < b e r > b , onde r é a distância ao centro da camada;

b ) Obtenha as cargas nas superfícies interna e externa da camada esférica e suas respectivas densidades de cargas nelas;

Passo 1

a ) Utilizando a Lei de Gauss, determine o campo elétrico E → r , para r < a ,   a < r < b e r > b , onde r é a distância ao centro da camada;

Antes de começar...

Esse problema é clássico de Lei de Gauss, que é dada por:

∯ G   E → ∙ d A → = Q i n t ϵ 0

Dada a geometria esférica do problema, podemos simplificar a Lei de Gauss:

E ∯ G   d A = Q i n t ϵ 0

E A = Q i n t ϵ 0

E = Q i n t ϵ 0 A

Onde A é a área da nossa gaussiana que, pelo geometria do problema, é uma esfera, logo:

E = 1 4 π ϵ 0 Q i n t r 2

O último detalhe aqui é que, novamente, pela geometria esférica do problema, o campo elétrico estará sempre na direção radial. Sendo assim:

E → = 1 4 π ϵ 0 Q i n t r 2 r ^

Agora, para cada caso, o nosso único trabalho é determinar a carga interna Q i n t .

Passo 2

-
  • r < a :

    • Essa região engloba apenas a carga pontual, logo:

    Q i n t = - 3 Q

    Portanto:

    E → = - 3 4 π ϵ 0 Q r 2 r ^

  • a < r < b :

    • Essa região engloba a carga pontual e a superfície interna da camada esférica... mas essa região está no interior do condutor, consegue ver?

    Então aqui vai algo pra você guardar sempre contigo... no interior de um condutor, o campo elétrico é sempre nulo.

    Portanto:

    E → = 0 →

  • r > b :

    • Essa região engloba tanto a carga puntiforme, quanto a camada esférica, logo:

    Q i n t = - 3 Q + 5 Q = 2 Q

    Portanto:

    E → = 2 4 π ϵ 0 Q r 2 r ^

    E → = 1 2 π ϵ 0 Q r 2 r ^

    Passo 3

    b ) Obtenha as cargas nas superfícies interna e externa da camada esférica e suas respectivas densidades de cargas nelas;

    Lembra que quando calculamos o campo elétrico na região a < r < b , dentro do condutor, eu disse que o campo elétrico ali é sempre nulo?

    Uma gaussiana nessa região, englobaria a esfera de carga puntiforme - 3 Q e a superfície interna da casca esférica condutora, de carga Q s u p . i n t . Assim, para que o campo elétrico seja nulo, necessariamente:

    Q i n t = 0

    Q i n t = - 3 Q + Q s u p . i n t = 0

    Q s u p . i n t = 3 Q

    Assim, a densidade superficial de carga da superfície interna será:

    σ s u p . i n t = 3 Q 4 π a 2

    Mas você concorda que a carga total da camada condutora deve ser igual a + 5 Q ?! (O enunciado que nos disse isso)

    A carga total da casca esférica vai ser a soma das cargas nas superfícies interna e externa:

    Q c a m a d a = 5 Q

    Q s u p . i n t + Q s u p . e x t = 5 Q

    3 Q + Q s u p . e x t = 5 Q

    Q s u p . e x t = 2 Q

    Assim, a densidade superficial de carga da superfície externa será:

    σ s u p . i n t = 2 Q 4 π b 2

    σ s u p . i n t = Q 2 π b 2

    Resposta

    a )

  • r < a :

    • E → = - 3 4 π ϵ 0 Q r 2 r ^

  • a < r < b :

    • E → = 0 →

  • r > b :

E → = 1 2 π ϵ 0 Q r 2 r ^

b )

Q s u p . i n t = 3 Q

σ s u p . i n t = 3 Q 4 π a 2

Q s u p . e x t = 2 Q

σ s u p . i n t = Q 2 π b 2

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

A Fig. 23-30 mostra uma superfície gaussiana com a forma de um cubo de 2,00 m de aresta, imersa em um campo elétrico dado porE → = 3,00 x + 4,00 i ^ + 6,00 j ^ + 7,00 k ^ N / C , com x em metros. Qual
Uma fina casca esférica não-condutora de raio R 1 tem carga total q 1 uniformemente distribuída em sua superfície. Uma segunda fina casca esférica não condutora e maior, de raio R 2 , coaxial com a pr
Uma esfera de raio R tem densidade volumétrica de carga ρ = B / r para rR , onde B é uma constante e ρ = 0 para rR . (a) Determine a carga total na esfera. (b) Determine as expressões par ao campo elé
Um cilindro sólido não condutor infinitamente longo de raio a tem uma massa específica volumétrico uniforme de ρ 0 . Mostre que o campo elétrico é dado pelas seguintes expressões: E R = ρ R / 2 ε 0 pa
Uma fina casca cilíndrica de comprimento 200m e raio 6,00c m tem uma densidade superificial uniforme de carga de 9,00n C / m 2 . (a) Qual é a carga total na casca? Determine o campo elétrico nas segui