Uma casca esférica condutora de raio interno e raio externo é carregada com carga , conforme a figura abaixo.
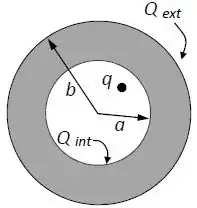
No interior do condutor há uma carga pontual . Denominamos por e , as cargas nas superfícies interna e externa do condutor, respectivamente, quando este chega ao equilíbrio.
Considere as afirmativas abaixo:
Se e , então, para , o campo elétrico aponta radialmente para fora e seu módulo é:
Se e , então, para , o campo elétrico aponta radialmente para dentro e seu módulo é:
Se e , então e .
Se e , então e .
Se as cargas e forem ambas positivas o campo elétrico dentro docondutor não será nulo.
São verdadeiras as afirmativas:
e;
e;
e;
e;
e;
e.
Passo 1
Vamos começar trabalhando com as cargas.
Sabemos que a relação entre as cargas , e é dada por:
Além disso, sabemos que no interior de um material condutor, o campo elétrico é sempre nulo. Dessa forma, aplicando o conceito à lei de Gauss, utilizando simetria esférica na região dentro da casca cilíndrica, teremos:
Assim, para o campo elétrico ser nulo, é necessário que a carga interna à gaussiana seja nula. Portanto:
Substituindo na primeira expressão, teremos:
Agora vamos quebrar a cabeça com as afirmações.
Passo 2
Se e , então, para , o campo elétrico aponta radialmente para fora e seu módulo é:
Aplicando a Lei de Gauss a esse problema e utilizando a simetria esférica, teremos:
Para :
Finalmente:
A afirmação é falsa.
Passo 3
Se e , então, para , o campo elétrico aponta radialmente para dentro e seu módulo é:
Novamente, para , teremos?
Assim, o campo elétrico será dado por:
Como , , logo:
Como o campo é negativo, ele aponta radialmente para dentro e o módulo do campo é:
A afirmação é verdadeira.
Passo 4
Se e , então e .
Para a superfície interna, temos que:
Para a superfície externa, temos que:
A afirmação é falsa.
Passo 5
Se e , então e .
Para a superfície interna, temos que:
Para a superfície externa, temos que:
A afirmação éverdadeira.
Passo 6
Se as cargas e forem ambas positivas o campo elétrico dentro do condutor não será nulo.
O campo elétrico no interior de um condutor é sempre nulo.
A afirmação é falsa.
Resposta
e;