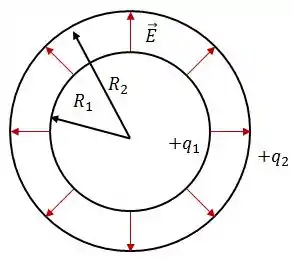
Uma casca esférica de raio tem uma carga total , uniformemente distribuída em sua superfície. Uma segunda casca esférica de raio , concêntrica com a primeira tem carga , também uniformemente distribuída em sua superfície.
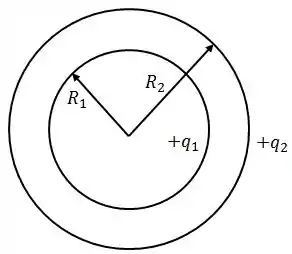
Utilize a Lei de Gauss para determinar o vetor campo elétrico nas regiões onde: , e ;
Qual seria a relação entre as cargas e seus sinais relativos para que o campo elétrico fosse nulo para ?
Esquematize as linhas de forças de campo elétrico para a situação quando a carga é positiva;
Passo 1
Utilize a Lei de Gauss para determinar o vetor campo elétrico nas regiões onde: , e ;
A Lei de Gauss é dada por:
Para problemas de geometria esférica, podemos simplificar a Lei de Gauss para:
Onde corresponde à área superficial da nossa gaussiana que, para problemas de geometria esférica, também é uma esfera.
Ou seja, para cada caso, a única coisa que temos que fazer é determinar o valor de .
Passo 2
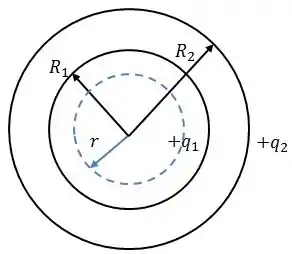
Para essa região, não temos nenhuma carga interna, logo:
Nessa região, a única carga que aparece dentro da nossa gaussiana é a carga . Sendo assim:
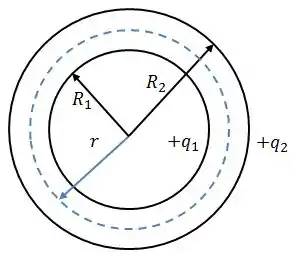
Essa região engloba as duas cascas esféricas, portanto:
Passo 3
Qual seria a relação entre as cargas e seus sinais relativos para que o campo elétrico fosse nulo para ?
O campo elétrico nessa região é dado por:
Assim, tem duas formas do campo elétrico ser nulo. A primeira é se (que não nos interessa)... a segunda é se:
Passo 4
Esquematize as linhas de forças de campo elétrico para a situação quando a carga é positiva;
Para a situação , nós teríamos campo elétrico somente na região , portanto, para positivo:
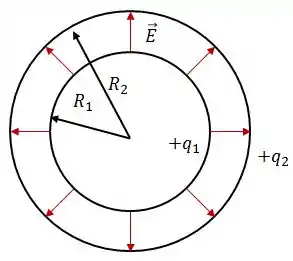
Resposta