Um cilindro maciço infinito, não condutor, de raio , apresenta uma densidade volumétrica de carga variável dada por :

onde é uma constante positiva e é a distância ao eixo de simetria do cilindro (veja figura abaixo). Nestas condições, calcule:

- A carga elétrica numa porção finita do cilindro, que tenha comprimento .
- O módulo do campo elétrico para .
- O módulo do campo elétrico para .
Passo 1
a) Para encontrarmos a carga total, precisamos notar que o elemento de volume infinitesimal nesse caso é dado por , como mostra a figura abaixo.
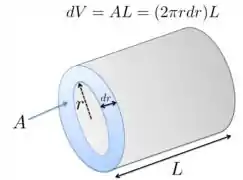
Portanto, substituindo a expressão para dada pelo problema, temos que
que resulta em
Passo 2
b) Para , temos a superfície gaussiana como mostra a figura abaixo. O campo elétrico aponta para fora do cilindro e tem o mesmo módulo em toda a área da superfície gaussiana com . Além disso, é sempre paralelo ao vetor na superfície lateral da gaussiana e sempre perpendicular às áreas das tampas. Portanto, só precisamos considerar as áreas laterais da gaussiana para o cálculo de .
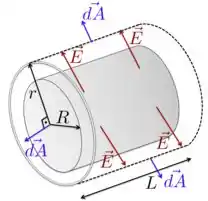
Colocando essas informações na lei de Gauss para , temos que
Simplificando essa expressão, obtemos
Passo 3
c) Para , podemos fazer as mesmas considerações no item b) para o campo sobre a superfície gaussiana cilíndrica. O único aspecto que precisamos ter atenção agora é que dentro do volume da gaussiana não temos mais a carga total. Por isso, precisamos ver quanto de carga tem no volume dentro da região para sabermos como é o módulo do campo que essa carga produz.
Para isso, podemos tomar a expressão que desenvolvemos no item a), mudando, agora, os limites de integração, ou seja,
Simplificando essa expressão, temos:
Aplicando a lei de Gauss para , temos:
que nos dá: