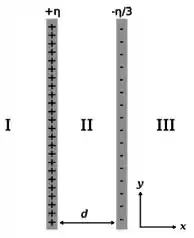
Dois planos muito grandes, homogeneamente carregados, um com e outro com , estão separados por uma distância como mostra a figura. Assinale a opção que especifica, corretamente, o módulo, direção e sentido do campo elétrico na região I:
Passo 1
Para matar essa questão, a gente precisa se lembrar de como são os campos elétricos gerados por planos “infinitos” e, particular, como são esses campos produzidos nas regiões a esquerda de cada plano, já que o problema pede para encontrarmos o campo resultante apenas na região I da figura.
Para começar, o vetor campo elétrico produzido pelo plano positivo com carga na região I é:
que tem direção e sentido de , já que a carga positiva do plano produz um campo elétrico afasta do plano.
Passo 2
Agora, o campo elétrico produzido pelo plano infinito negativo com carga na região será:
que aponta na direção e sentido de , pois o campo elétrico produzido pelo plano negativo está orientado no sentido de se aproximar desse plano.
Passo 3
Bom, agora que já temos os campos e produzidos pelas cargas positivas e negativas dos planos, respectivamente, podemos calcular o campo elétrico resultante na região I, que a soma vetorial desses dois campos.
Portanto, o campo resultante será:
Resposta
Letra e.