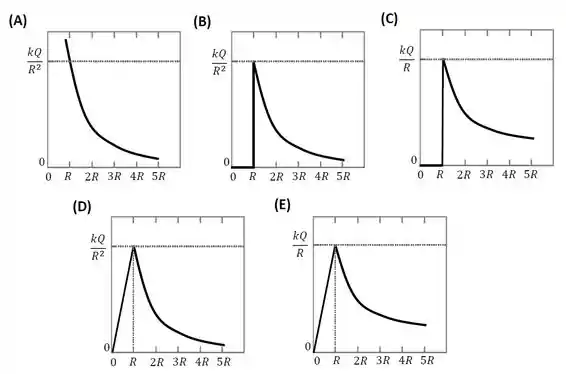
Uma esfera maciça de raio , feita de material condutor, está carregada com uma carga . Se representa o módulo do campo elétrico gerado pela esfera carregada, onde é a distância ao centro da esfera, o gráfico que reproduz a função CORRETAMENTE é:
Passo 1
Primeiramente, vamos entender nosso problema.
O exercício pede para determinarmos o gráfico do módulo do campo elétrico gerado por uma esfera maciça condutora com carga em função da distância até o centro da esfera.
Para sabermos o gráfico, precisamos saber como é a expressão para o campo elétrico em questão, tanto dentro, quanto fora da esfera.
Assim, imediatamente, temos que o campo elétrico DENTRO da esfera é zero!
UÉÉÉ!!!! COMO ASSIM?!!?!?!
Calma, vou explicar. O enunciado diz que a esfera é feita de um material condutor. Assim, o campo elétrico é SEMPRE NULO dentro de condutores. Você nem precisa se preocupar! :D
Daí, só falta o campo elétrico fora da esfera. Para determinar o campo elétrico fora da esfera, podemos utilizar a lei de Gauss na forma integral.
Esta lei diz que o fluxo de um campo elétrico por uma superfície fechada genérica é dada por
Na equação anterior, é a carga elétrica líquida dentro da superfície e um vetor unitário normal ao elemento infinitesimal de área . Esta superfície recebe o nome de superfície gaussiana.
A grande sacada de utilizar a lei de Gauss é que se tomarmos uma superfície gaussiana na qual o campo elétrico sobre ela possui módulo constante em todos os seus pontos, podemos retirar o módulo do campo elétrico da integral dupla anterior e isolá-lo.
A forma de escolher a superfície gaussiana se baseia na simetria do campo elétrico. Para o nosso caso, o campo elétrico é radial (só depende da distância até o centro da esfera). Assim, a superfície gaussiana perfeita para o uso são cascas esféricas.Agora que traçamos nossa estratégia, vamos aos cálculos!
Passo 2
Para calcular o campo elétrico fora da esfera, considere a seguinte superfície gaussiana.
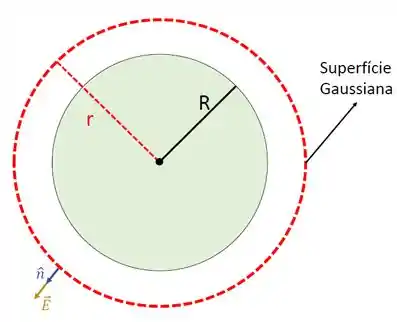
Na figura anterior, a esfera maciça condutora está totalmente dentro da superfície gaussiana de raio , com . O campo elétrico é radial e constante sobre a superfície gaussiana.
Assim, pela lei de Gauss, temos que
com a área total da superfície gaussiana dada por
A carga interna é toda carga da esfera, pois a esfera toda está dentro da superfície gaussiana. Assim,
Logo,
com a constante eletrostática (ou de Coulomb) dada por
Portanto, o campo elétrico fora da esfera é proporcional a .
Assim, no próximo passo, faremos o gráfico do campo elétrico dentro e fora da esfera.
Passo 3
Mostramos nos passos anteriores que o módulo do campo elétrico da esfera maciça é
Assim, temos as seguintes informações:
- O módulo do campo elétrico DENTRO da esfera é nulo pois a esfera é feita de material condutor;
- Fora da esfera, o módulo do campo elétrico diminui com o inverso do quadrado da distância . Para distâncias muito grandes, o módulo do campo tende a zero.
Portanto, o gráfico do módulo do campo elétrico é
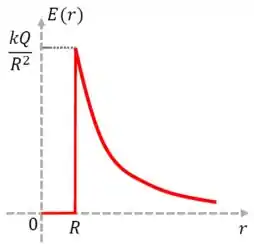
Analisando as opções, vemos que a alternativa correta é a letra .