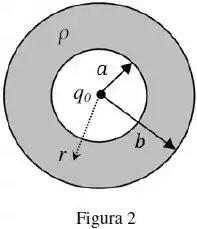
A figura 2 ilustra uma casca esférica não-condutora de raio interno e raio externo que possui uma densidade volumétrica de carga positiva constante . Uma carga elétrica pontual positiva está situada no centro da casca.
Na figura 2, representa a distância ao centro da casca esférica.
Para este arranjo eletrostático, calcule:
A carga total do sistema.
O vetor campo elétrico em todas as regiões do espaço: ; ; .
Passo 1
A carga total do sistema.
A carga total do sistema será igual à soma da carga pontual com a carga da casca esférica, logo:
Onde a carga da casca esférica é dada por:
Como a densidade volumétrica de carga é constante, podemos tirá-la da integral, logo:
Onde a integral abaixo representa o volume da casca esférica, logo:
Portanto, a carga total do sistema será:
Passo 2
O vetor campo elétrico em todas as regiões do espaço: ; ; .
O campo elétrico pode ser calculado através da lei de Gauss, dada por:
Utilizando a simetria esférica do problema, podemos reescrever a integral da seguinte forma:
Agora, para cada caso, basta calcular a carga no interior da nossa gaussiana.
Passo 3
;
Nessa região, a gaussiana engloba somente a carga pontual, logo:
;
Aqui a gaussiana engloba a carga pontual e uma parte da casca esférica.
Seguindo o mesmo raciocínio que usamos na letra para calcular a carga total da casca esférica, teremos:
Logo:
Reorganizando isso, teremos:
;
A gaussiana agora engloba todo o sistema. Dessa forma:
Resposta