A figura mostra o campo elétrico gerado por um dipolo elétrico. Determine o fluxo elétrico através da superfície
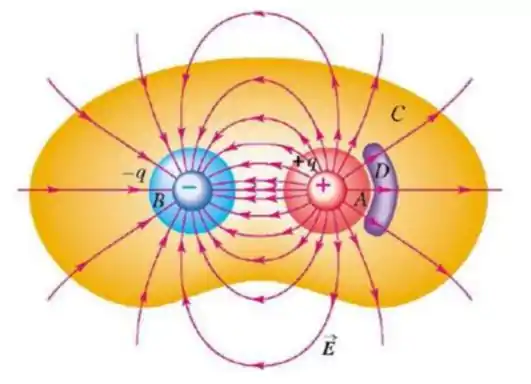
Passo 1
Tem uma lei muito importante que nos permite determinar o fluxo elétrico, você se lembra qual? É a lei de Gauss né?! Então, pela lei de Gauss, temos que
Onde representa a carga no interior da superfície gaussiana. Nesse caso, temos que a superfície gaussiana é uma superfície que está no exterior de , então, dentro da superfícia gaussiana temos uma carga de e uma de , ou seja, a carga no interior é . Entao, pela lei de Gauss
O fluxo elétrico é nulo
Resposta
O fluxo elétrico é nulo