A figura mostra a visão de perfil de três placas não condutoras de grande extensão densidades superficiais uniforme de cargas com valores , e (). Usando o princípio da superposição, determine
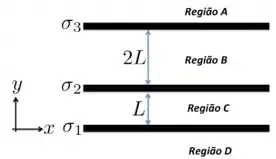
- O vetor campo elétrico nas regiões A, B, C e D;
- A diferença de potencial entre as placas com densidades e ;
- O trabalho do campo elétrico quando um elétron é deslocado entre as placas com densidade e .
Passo 1
Como temos três placas “de grande extensão”, o campo que elas produzem é perpendicular às respectivas superfícies e constante em todo o espaço. Se as cargas das placas forem positivas, as linhas de campo estarão no sentido de se afastarem das placas, e se forem negativas, no sentido de se aproximarem das placas.
Para facilitar a nova análise, dá uma olhada na figura abaixo, em que representamos as placas separadamente e seus respectivos campos elétricos, considerando a orientação do eixo dado.

Vamos somar vetorialmente os campos elétricos produzidos pelas placas em cada uma das regiões. Antes, o módulo campo elétrico produzido por uma placa de “grande extensão” (ou “infinita”) e com densidade superficial de carga é:
Vamos aplicar essa expressão, junto com as respectivas direções e sentidos dos campos, para obter o campo resultante em cada região da figura.
Passo 2
a) Na região A (RA), temos, olhando para a figura acima, que o campo resultante será:
Na região B (RB):
Na região C (RC):
Na região D (RD):
Repara que a única coisa que fizemos foi somar os vetores nas regiões considerando os campo dados na figura acima para cada uma das placas condutoras.
Passo 3
b) Agora, para começar este item, precisamos olhar para o campo resultante nas regiões B e C e somá-los. Nesse caso, o campo resultante será:
Como só temos campo elétrico na direção , o campo elétrico está relacionado com o potencial através da seguinte relação:
Portanto, se e , então a diferença de potencial entre as placas e será:
Passo 4
c) Na região B, temos um campo elétrico resultante dado por:
Agora, vamos considerar a figura abaixo, na qual representamos as placas e e o campo entre elas. Além disso, o elétron parte de uma posição inicial e vai até uma posição final no sentido contrário ao campo elétrico .
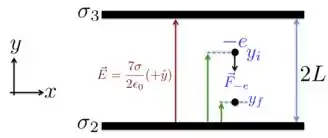
O trabalho realizado pelo campo elétrico sobre o elétron é:
Como o campo elétrico nessa região é uniforme, então teremos que:
Portanto, esse é o trabalho realizado pelo campo para levar o elétron de um ponto arbitrário até um outro ponto dentro da região entre as placas e .