Medidas na superfície de nosso planeta, cujo raio médio é , sugerem que o campo elétrico aí é orientado para baixo e que o valor médio de sua componente normal é . Aceitas tais informações e considerando que , qual valor abaixo melhor aproxima a carga total de nosso planeta?
(a) .
(b) .
(c) .
(d)
(e) , pois a Terra é neutra, senão levaríamos choques elétricos o tempo todo.
(f)
(g)
Passo 1
Lendo o enunciado com atenção vemos que ele fala que o campo na superfície é orientado para baixo. Isso quer dizer que a carga do planeta é negativa. Pois as cragas negativas apresentam um campo elétrico “entrando”, já as cargas positivas apresentam um campo elétrico “saindo”.
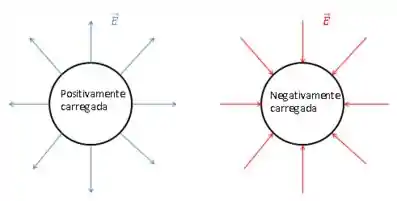
Então,
Com isso, já eliminamos todas as alternativas positivas.
Passo 2
Bom, temos um corpo esférico (Terra) carregado. Usando a lei de Gauss, com uma superfície gaussiana esférica, temos:
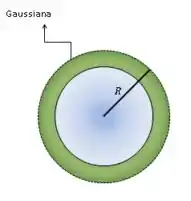
A integral é feita sobre a área da superfície gaussiana. Mas pensa só o vetor área aponta pra fora da superficie, e vetor campo aponta para dentro, então o ângulo entre eles é , e portanto,. A carga está distribuída de forma uniforme, então podemos tirar ele da integral, porque ele não varia com a área.
Agora, temos que integrar a área da superficie gaussiana. Que é uma esfera de raio .
Ok... Mas olha só. Ele falou pra gente o valor de , mas a gente precisa de . E agora? Nada de desespero. Eles estão relacionados!
Pronto!
Voltando lá.
Substituindo
Resolvendo
Resposta
Letra b).