Uma partícula de carga é colocada no centro de um condutor em formato de casca esférica, de raios interno e externo , carregado com carga total . A situação é mostrada na figura abaixo.
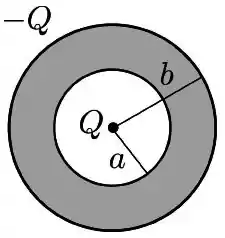
Sabe-se ainda que o sistema está em equilíbrio eletrostático.
Utilizando a lei de Gauss, determine o campo elétrico (módulo, direção e sentido) nas regiões do espaço definidas por , e , onde é a distância ao centro da casca. Esboce o gráfico de sua intensidade como função de .
Determine a densidade superficial de carga nas superfícies interna e externa da casca condutora.
Num ponto distando do centro do condutor é colocada e fixada uma partícula de carga Q. Após reestabelecido o equilíbrio eletrostático no condutor, a força elétrica sobre essa nova carga será atrativa, repulsiva ou nula? Justifique sua resposta.
Passo 1
Utilizando a lei de Gauss, determine o campo elétrico (módulo, direção e sentido) nas regiões do espaço definidas por , e , onde é a distância ao centro da casca. Esboce o gráfico de sua intensidade como função de .
A Lei de Gauss é dada por:
Como estamos trabalhando com um corpo com simetria esférica, vamos utilizar como gaussiana uma esfera com raio genérico .
Fazendo isso, os vetores e serão paralelos em todos os pontos da gaussiana, além disso, o módulo do campo elétrico será o mesmo em todos os pontos da gaussiana.
Dessa forma, podemos escrever a Lei de Gauss da seguinte forma:
Onde corresponde à área da nossa gaussiana esférica.
Finalmente, basta calcular a carga englobada pela gaussiana em cada caso.
Passo 2
- :
- :
- :
A gaussiana aqui se encontra no interior da cavidade esférica, englobando somente a carga pontual , dessa forma:
Assim, o vetor campo elétrico será dado por:
Essa região corresponde ao interior da casca condutora. E aqui vai algo que você precisa guardar no coração:
O campo elétrico no interior de um condutor é sempre igual a zero.
Dessa forma:
Finalmente, a gaussiana agora engloba tanto a carga pontual , quanto toda a casca esférica com carga , logo:
Substituindo isso na equação do campo elétrico, teremos:
Passo 3
Agora temos que esboçar esse campo elétrico! Vimos que
Assim o nosso esboço fica
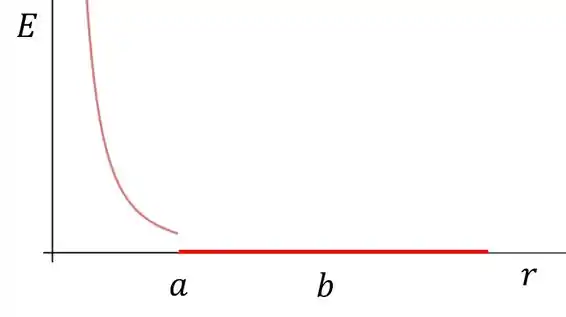
Lembrando que o campo para é positivo por que a carga é positiva 😉
Passo 4
Determine a densidade superficial de carga nas superfícies interna e externa da casca condutora.
Por definição, a densidade superficial de carga é dada por:
Como estamos trabalhando com superfícies esféricas, temos que:
Então o nosso trabalho aqui é determinar a carga em cada uma das superfícies.
Como temos uma carga pontual na cavidade da casca esférica, será induzida uma carga (mesmo módulo, mas sinal oposto ao da carga pontual) na superfície interna (de raio ), logo:
Ok! Sabemos a carga na superfície interna e sabemos que a carga total da casca esférica vale , sendo assim, a carga na superfície externa :
Finalmente:
Passo 5
Num ponto distando do centro do condutor é colocada e fixada uma partícula de carga . Após reestabelecido o equilíbrio eletrostático no condutor, a força elétrica sobre essa nova carga será atrativa, repulsiva ou nula? Justifique sua resposta.
Essa questão é um pouco dibrosa.
Já vimos que nessa região o campo elétrico é nulo e que, além disso, a carga é nula na superfície externa da casca esférica.
No entanto, mesmo com a carga sendo nula na superfície externa, a presenta da partícula de carga irá induzir uma concentração de cargas negativas na região próxima à partícula, enquanto teremos cargas positivas do outro lado da casca.
A força de atração entre a partícula e as cargas polarizadas mais próximas à partícula (por conta da menor distância) será maior que a força de repulsão entre a partícula e as cargas polarizadas mais afastadas dela.
Finalmente, a força sobre essa nova carga será atrativa.
Resposta
A força sobre essa nova carga será atrativa.