Uma placa isolante, com espessura e densidade volumétrica de carga uniforme igual a , está separada de uma outra placa, condutora, com carga total igual a zero e de espessura . As duas placas são infinitas nas direções e , conforme a figura.
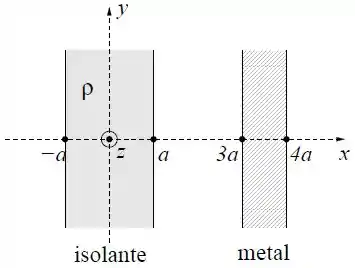
Use a lei de Gauss para calcular o vetor campo elétrico produzido pela placa isolante em um ponto dentro da placa, isto é um ponto com coordenada .
Use a lei de Gauss para calcular o vetor campo elétrico produzido pela placa isolante em um ponto fora dela.
Calcule, em termos de e , a densidade superficial de cargas induzidas nas superfícies da placa condutora após o equilíbrio eletrostático ter sido atingido. Determine em todo o espaço o campo elétrico resultante devido ao isolante e ao condutor.
Passo 1
Use a lei de Gauss para calcular o vetor campo elétrico produzido pela placa isolante em um ponto dentro da placa, isto é um ponto com coordenada .
Devido à simetria do problema, é possível ver que o campo elétrico gerado pela placa estará sempre na direção do eixo .
Assim, as nossas gaussianas serão todas paralelepípedos, onde o campo elétrico no interior das placas, onde há fluxo elétrico apenas pelas faces paralelas às superfícies da placa.
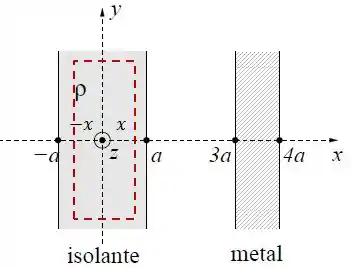
A Lei de Gauss é dada por:
Como o campo elétrico é uniforme sobre as superfície em que cruza a gaussiana e ele cruza a gaussiana através de duas faces, podemos simplificar a Lei de Gauss para:
Agora o nosso trabalho é apenas calcular a carga interna . Pra isso, vamos usar a densidade volumétrica de carga, dada pelo problema:
Portanto:
Passo 2
Use a lei de Gauss para calcular o vetor campo elétrico produzido pela placa isolante em um ponto fora dela.
A geometria do problema permanece a mesma, a diferença agora é que a carga interna agora será a carga total da placa.
Agora o campo elétrico é dado por:
Passo 3
Calcule, em termos de e , a densidade superficial de cargas induzidas nas superfícies da placa condutora após o equilíbrio eletrostático ter sido atingido. Determine em todo o espaço o campo elétrico resultante devido ao isolante e ao condutor.
O campo elétrico gerado pela placa isolante vai induzir uma polarização na placa isolante.
As cargas positivas tendem a se mover no mesmo sentido do campo que age sobre elas e as cargas negativas tendem a se mover no sentido oposto. Como o campo elétrico está “saindo” da placa isolante, ou seja, , as concentrações de cargas positivas e negativas terão essa cara:
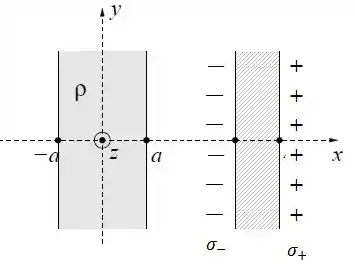
Assim, a densidade de carga induzida vai gerar um campo elétrico induzido que, por conta da polarização, terá o seguinte sentido:
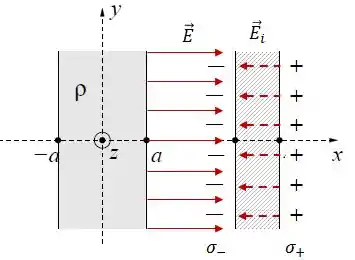
Como o campo elétrico é nulo no interior de qualquer condutor, no interior desse condutor:
O campo elétrico induzido é a soma dos campos elétricos gerados pelas superfícies positiva e negativa do condutor:
Onde:
Portanto:
Por fim:
Resposta