Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema Fundamental do Cálculo

Ver Teoria
Exercício 771234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757678798081828384858687888990919293949596979899100

Enunciado

UFRJ - Cálculo 1 - Listas do AVA - Lista 15 - TFC - 4b

a. Seja f ( x ) contínua. Existe uma função g ( x ) com g ’ ( x )   =   f ( x ) e g ( 0 )   =   7 ? Existe uma função h ( x ) com h ’ ( x )   =   f ( x ) ² e h ( 1 )   =   - 1 ?

b. Seja f ( x ) derivável. Existe uma função g ( x ) com g ’ ’   ( x )   =   f   ‘ ( x ) ,   g ’   ( 0 )   =   0 , e g ( 0 )   =   1 ?

c. Existe h ( x ) derivável com h ’ ( x ) ²   = 4 π e - 2 x ² ?

Passo 1

Vamo pra cima galera! Como aqui é uma questão que envolve uma teoria muito pesada, vamos seccionar em algumas partes dentro dos passos. Começando pelo item a):

Seja f ( x ) contínua. Existe uma função g ( x ) com g ’ ( x )   =   f ( x ) e g ( 0 )   =   7 ?

Queremos uma função que aplicada em 0 seja 7 e cuja derivada seja uma função contínua. Difícil imaginar isso? Vamos escrever ela usando uma função polinomial que é muito comum para esse tipo de derivada.

g x = x 2 + 7

g 0 = 0 2 + 7 = 7

g ' x = 2 x

Sabendo que g ' x = 2 x continua sendo uma função polinomial e, portanto, contínua, podemos dizer que a resposta da pergunta é sim.

Outro exemplo seria:

g x = s e n ( x ) + 7

g 0 = s e n 0 + 7

0 + 7 = 7

g ' x = c o s ⁡ ( x )

Passo 2

Agora vamos pra próxima pergunta do item a).

Seja f ( x ) contínua. Existe uma função h ( x ) com h ’ ( x )   =   f ( x ) ² e h ( 1 )   =   - 1 ?

Queremos uma função que aplicada em 1 seja -1 e cuja derivada seja uma função contínua elevada ao quadrado. Podemos novamente usar uma função polinomial, mas agora quando queremos que a derivada esteja elevada ao quadrado, na variável a ser derivada vamos usar ela com um expoente maior.

h x = x ³ - 2

h 1 = 1 ³ - 2

h ( 1 ) = - 1

h ' x = 3 x ²

f x = 3 x ²

f ( x ) = 3 x

Sabendo que f ( x ) = 3 x continua sendo uma função polinomial e, portanto, contínua, podemos dizer que a resposta da pergunta é sim.

Passo 3

Aqui no item b), a questão tenta pregar uma peça, mas a gente é mais esperto. Se liga:

Seja f ( x ) derivável. Existe uma função g ( x ) com g ’ ’   ( x )   =   f   ‘ ( x ) ,   g ’   ( 0 )   =   0 , e g ( 0 )   =   1 ?

Ora, queremos uma função g ( x ) que aplicada em 0 resulte em 1, cuja derivada primeira aplicada em 0 resulte em 0, e sua derivada segunda seja igual à derivada primeira de uma função f ( x ) . Aqui vamos usar uma função trigonométrica, porque elas variam os sinais quando a gente integra/deriva e isso pode ajudar demais. Vamo lá:

g x = c o s   x  

g 0 = c o s   0  

g(0) = 1

g ' x = - s e n x

g ' 0 = - s e n 0

g ' ( 0 ) = 0

g ’ ’   x =   - c o s   x  

→   f x =   - s e n x

Sabendo que f ' x = -   s e n   x   é derivável, a resposta então é sim.

Passo 4

Agora vamos resolver esse último item e detonar a questão!

Existe h ( x ) derivável com h ’ ( x ) ²   = 4 π e - 2 x ² ?

Eita que monstrinho hein? Mas vamos mastigar ela aqui com calma. Sabendo que a função h ’ ( x ) ² tem esse formato, primeiro vamos tirar essa potência dela:

h ' x = 4 π e - 2 x ²  

h ' ( x ) = 2 π e - x ²

Agora, pra gente enxergar o h x natural, vamos integrar isso!

h x = 2 π ∫ e - x ² d x

A resolução dessa integral não é trivial e portanto pra questão acredito que não vale a pena a gente estender mais. Porém, podemos observar que a função integrada é contínua em todo o domínio dos reais.

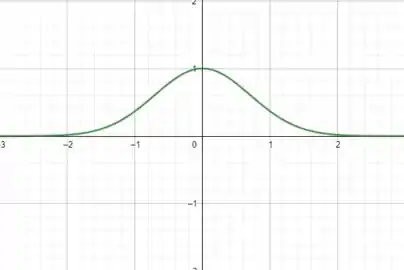
Portanto, a integral existe e h ( x ) contínua também.

Resposta

a. Sim a todas as perguntas.

b. Sim

c. Sim

Exercícios de Livros Relacionados

Use a parte 1 do teorema fundamental do cálculo para encontrar a derivada da função: h x = ∫ 2 1 / x arctan ⁡ t d t
Ache a integral indefinida geral. Ilustre fazendo o gráfico de vários membros da família na mesma tela. ∫ cos ⁡ x - 2 sen ⁡ ( x ) d x
Cada uma das seguintes funções resolve um dos problemas de valor inicial dos Exercícios 65-68. Qual função resolve qual problema? Justifique brevemente suas respostas. y = ∫ 1 x 1 t d t - 3 y = ∫ 0 x
A região no primeiro quadrante, limitada pela curva y = 5 - x x + 1 2 , pelo eixo x e pelo eixo y gira em torno do eixo x . Ache o volume do sólido gerado.
Em uma cidade com 12000 pessoas, a taxa de crescimento de uma epidemia de gripe é conjuntamente proporcional ao número de pessoas tiveram a gripe e ao número de pessoas que não a contraíram. Cinco dia