Considere a função
Determine os dois pontos críticos de , isto é, os pontos onde .
Identifique qual desses pontos é ponto de máximo e qual é ponto de mínimo. Justifique.
Passo 1
Bom, para achar onde é nulo precisamos, inicialmente, derivar . Como esse cara é definido por uma integral, vamos usar o Teorema Fundamental do Cálculo para derivá-lo:
Repara o seguinte: a exponencial é sempre positiva. O sinal de , portanto, só vai depender de ! Os dois pontos que zeram esse termo, suas raízes, são e .
Dessa maneira, os dois pontos críticos de são e !
Passo 2
Para observar se os pontos são de máximo ou de mínimo temos que olhar para o sinal da derivada antes e depois de cada ponto. Vamos fazer o quadro de sinais para tirar essa dúvida:
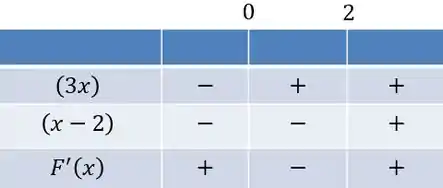
Dá para ver que o ponto crítico do tem derivada positiva antes e negativa depois, o que gera um ponto de máximo. Já o do tem derivada negativa antes e positiva depois, sendo esse um ponto de mínimo, portanto.
Logo, é ponto de máximo local e de mínimo local.