Teorema Fundamental do cálculo
Seja
Determine os intervalor onde é crescente.
Passo 1
Para vermos quando a função é crescente precisamos olhar o sinal da sua derivada. Vamos derivar essa função
Temos uma função no limite de integração, lembra que quando usamos o teorema fundamental do cálculo aqui temos que fazer
Que é multiplicar a derivada da função que está no limite de integração pela função da integral. Além disso o que vai dentro da função de é a função no limite de integração.
Passo 2
Temos que analisar o sinal da função
Repara que vai ser sempre maior que , isso porque e no denominador temos , e esse cara é maior ou igual a
Beleza então temos que ver o sinal de
Podemos reescrever isso lembrando de produto notável
E sabemos que e só tem uma raiz, vamos ver o seu quadro de sinais
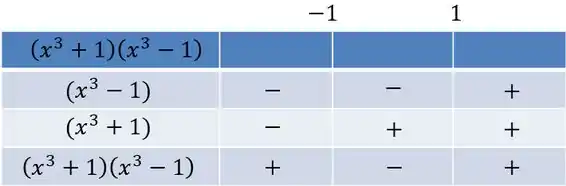
Isso nos diz que quando ou a derivada vai ter sinal positivo, ou seja vai ser crescente.