ME04) Seja uma função contínua cujo gráfico está representado abaixo:
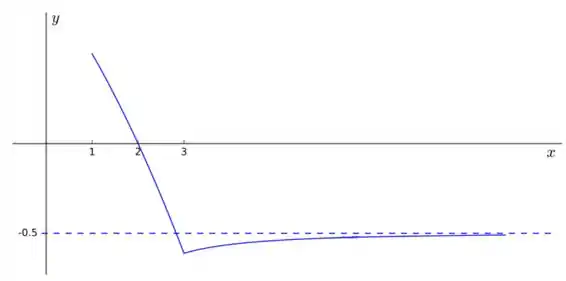
Considere as informações sobre a função:
Com :
- é crescente em e decrescente em
- é contínua, mas não é derivável
É correto dizer que:
- As afirmações e são verdadeiras
- Todas as afirmações são verdadeiras
- As afirmações e são verdadeiras
- Todas as afirmações são falsas
- As afirmações e são verdadeiras
Passo 1
A primeira coisa a se notar nessa questão é que muitas informações sobre a natureza de estão sendo pedidas. Apesar de não sabermos exatamente quem é , se conhecermos sua primeira derivada, podemos conversar sobre invervalos de crescimento e decrescimento. Seja a Teorema Fundamental do Cálculo dado por:
Para:
Vamos ter:
E usando isso, respondemos a questão. Vamos ver cada uma das afirmativas então, beleza?
Passo 2
é crescente em e decrescente em
Veja bem, como:
E o sinal da primeira derivada indica a inclinação da reta tangente, se olharmos com calma o gráfico do enunciado, vemos que em
E que em :
Como inclinação positiva quer dizer função crescente e inclinação negativa quer dizer função decrescente, então a afirmativa está corretíssima. Bora pra próxima:
Passo 3
é contínua, mas não é derivável
Novamente a gente vai usar:
Saca só, como é contínua em todo ponto, vídeo gráfico, então também é contínua em todo ponto. Se a derivada de é uma função contínua em todos os pontos, então é diferenciável com certeza e, por consequência, se é diferenciável então é contínua. Isso tudo nos mostra que dessa vez a afirmativa foi falsa! Bora pra última então:
Passo 4
Agora pra fechar com chave de ouro, vamos ver a última afirmativa. Usando pela última vez:
E olhando o gráfico, a gente bem vê que:
E como nos dá a inclinação da reta tangente de , como no limite essa inclinação tende a um número negativo, é como se fosse decrescente pra sempre nesse limite. Opa, já que é assim, essa afirmativa é verdadeira!
Como as afirmativas e são verdadeiras, a resposta vai ser a letra A