Teorema Fundamental do Cálculo
Considere:
Onde é a função cujo gráfico é dado abaixo:
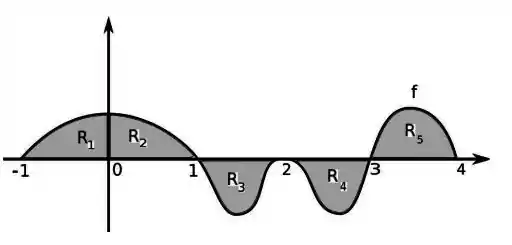
Sabendo que as áreas das regiões , , , e são:
, , , e .
Determine os intervalos de crescimento da função .
Passo 1
Sabemos que os intervalos de crescimento da função são quando sua derivada é positiva. Pelo teorema fundamental da álgebra:
Ou seja, em todo o intervalo que for positiva, teremos crescente. Olhando o gráfico, isto acontece quando:
Resposta
Exercícios de Livros Relacionados
Use a parte 1 do teorema fundamental do cálculo para encontrar a derivada da função: h x = ∫ 2 1 / x arctan t d t
Ache a integral indefinida geral. Ilustre fazendo o gráfico de vários membros da família na mesma tela. ∫ cos x - 2 sen ( x ) d x
Cada uma das seguintes funções resolve um dos problemas de valor inicial dos Exercícios 65-68. Qual função resolve qual problema? Justifique brevemente suas respostas. y = ∫ 1 x 1 t d t - 3 y = ∫ 0 x
A região no primeiro quadrante, limitada pela curva y = 5 - x x + 1 2 , pelo eixo x e pelo eixo y gira em torno do eixo x . Ache o volume do sólido gerado.
Em uma cidade com 12000 pessoas, a taxa de crescimento de uma epidemia de gripe é conjuntamente proporcional ao número de pessoas tiveram a gripe e ao número de pessoas que não a contraíram. Cinco dia