Teorema fundamental do Cálculo
Seja
É dado que
- Determine
- Ache a área do triangulo limitado pelos eixos e pela reta tangente ao gráfico de no ponto .
Passo 1
Normalmente quanto derivamos, o está no limite superior, mas dessa vez não está, mas lembra das propriedades de integral? Podemos fazer
Então vamos ver a função como
E vamos derivar usando o teorema fundamental do cálculo
Lembra que começar com ou , no limite inferior não faz diferença.
Passo 2
Vamos agora fazer
Passo 3
Para acharmos essa área, primeiro temos que achar a reta tangente.
Lembrando que a reta tangente em um ponto, no caso , vai ser
A derivada já achamos, e ele deu que é trocar por na integral, então vamos ter
Vamos ver como fica o esboço da reta,
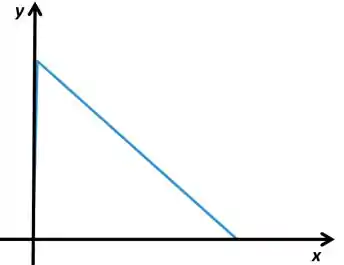
Isso vai ficar assim por o coeficiente de é negativo. Temos que achar os catetos desse triangulo, um vai ser onde e outro vai ser onde
Vamos começar fazendo
Um dos catetos é
Vamos fazer agora
O outro cateto vai ser
A área vai ser