Teorema Fundamental do Cálculo
Considere:
Onde é a função cujo gráfico é dado abaixo:
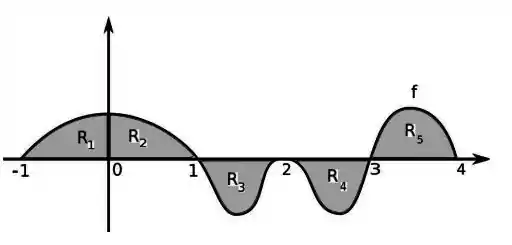
Sabendo que as áreas das regiões , , , e são:
, , , e .
Determine os pontos de máximo e mínimo local da função .
Passo 1
O máximo e mínimo da função ocorrem quando sua derivada é igual à zero. Igualamos utilizando o teorema fundamental da álgebra:
Pelo gráfico, observamos que:
Passo 2
Agora, vamos avaliar se o ponto é de máximo ou mínimo. Em não podemos saber, mas em sabemos que a derivada era positiva e passa à ser negativa. Ou seja, a função estava crescendo e passa à decrescer. Segue que é um ponto de máximo local.
Passo 3
O outro ponto , temos que a derivada era negativa antes e continua a ser negativa depois, portanto temos um ponto de sela.
Passo 4
Em temos que a derivada era negativa antes e virou positiva depois, portanto a função estava crescendo e começou à crescer, logo é um ponto de mínimo local. O último ponto () não podemos dizer nada.b
Portanto, chegamos à resposta.
Resposta
Máximo local é .
Mínimo local é .
Ponto de sela é .
Os outros dois pontos (, ) não podemos determinar, mas são pontos de máximo ou mínimo locais.