Teorema Fundamental do Cálculo
Considere definida por . Na figura abaixo, representa a área da região indicada e é a área do triângulo com vértices em , e indicado.
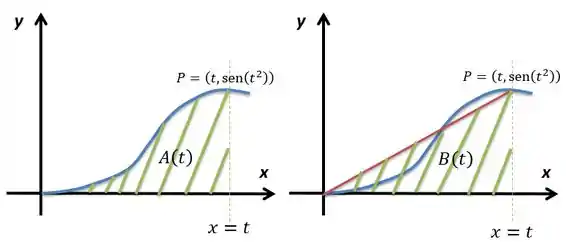
Determine .
Passo 1
Vamos resolver essa questão com calma, começando primeiro definindo quem seriam esses e .
Segundo a primeira imagem, é a área de de até um ponto qualquer. Seria isso daqui:
Já o é simplesmente a área do triângulo com um vértice na origem, um em e outro em . Sua base é e sua altura é , então a área do triângulo será:
Assim, o limite que nos interessa é:
Passo 2
Vamos resolver o limite agora. Repara que ao substituir o terá os limites de integração iguais, o que faz com que vá a , bem como será o ao substituir o valor:
Assim, como caímos numa indeterminação, podemos usar L’Hospital:
Derivando o denominador nós usamos o Teorema Fundamental do Cálculo; para o denominador usamos a Regra do Produto e da Cadeia:
Passo 3
Vou calcular o inverso desse limite e depois eu desinverto o resultado e jogo nessa última expressão que achamos.
Vamos concentrar só nesse limite que sobrou:
Podemos usar L’Hospital nele, já que caímos em outra indeterminação:
Então:
Passo 4
Voltando ao limite original, ou seja, desinvertendo esse, achamos a resposta final:
E essa é, finalmente, a nossa resposta!