Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Green

Ver Teoria
Exercício 971234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969899100

Enunciado

UFU, Sem Campus, Cálculo 3, Listas de C3 - Profª Laís Rodrigues - 1ª Lista - Integrais de Linha e de Superfície, Questão 10

Use o Teorema de Green para calcular a integral de linha ∮ C x y 2 d x + 2 x ² y d y , onde C é o triângulo com vértices 0,0   ,   2,2   e   ( 2,4 ) com orientação positiva

Passo 1

Fala aí galera, bora resolver o nosso exercício?

Para usarmos o Teorema de Green, vamos usar a seguinte relação:

∮ Ϭ D F 1 d x + F 2 d y = ∬ D d F 2 d x - d F 1 d y d x d y

E no caso, D vai ser nossa curva delimitando a função. A nossa curva vai ser justamente a região do nosso triângulo. Se a gente marcar os vértices do nosso triângulo, vamos achar:

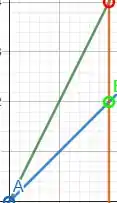
E por meio dessa região, vamos achar as funções para calcular nossa integral.

Passo 2

Vamos começar calculando as derivadas da nossa primeira fórmula:

∮ C x y 2 d x + 2 x ² y d y

∮ Ϭ D F 1 d x + F 2 d y = ∬ D d F 2 d x - d F 1 d y d x d y

Com isso, vamos dizer que:

F 1 = x y ²

F 2 = 2 x ² y

Show, agora vamos derivar:

d F 2 d x = 4 x y

d F 1 d y = 2 x y

Substituindo:

∮ C x y 2 d x + 2 x ² y d y = ∬ D 4 x y - 2 x y d x d y

∮ C x y 2 d x + 2 x ² y d y = 2 ∬ D x y d x d y

Show, agora precisamos saber os intervalos de integração.

Passo 3

Vamos olhar para a nossa figura:

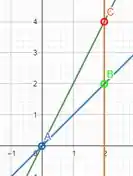
Se a gente for encontrar as funções que montam o nosso triângulo, teremos:

y = 2 x

y = x

Então:

x ≤ y ≤ 2 x

Show, e se olharmos para os valores de x , teremos:

0 ≤ x ≤ 2

Jogando na nossa integral:

2 ∬ D x y d x d y = 2 ∫ 0 2 ∫ x 2 x x y d y d x

Show, agora precisamos resolver as integrais.

Passo 4

Calculando, começando pela integral de dentro:

2 ∫ 0 2 ∫ x 2 x x y d y d x = 2 ∫ 0 2 x y 2 2 x 2 x d x

2 ∫ 0 2 ∫ x 2 x x y d y d x = ∫ 0 2 x y 2 x 2 x d x

2 ∫ 0 2 ∫ x 2 x x y d y d x = 3 ∫ 0 2 ( x 3 ) d x

Show, agora para a segunda integral:

2 ∫ 0 2 ∫ x 2 x x y d y d x = 3 4 x 4 0 2

2 ∫ 0 2 ∫ x 2 x x y d y d x = 12

Resposta

12

Exercícios de Livros Relacionados

Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . x 2 y 2 d x + x y d y C consiste num arco de parábola y = x 2 indo de ( 0,0 ) para ( 1,1 ) e o
Utilize o Teorema de Green para demonstrar a fórmula de mudança de variáveis para as integrais duplas (Fórmula 15.9.9) para o caso onde f x , y = 1 : ∬ R d xd y = ∬ S ∂ x , y ∂ u , v d ud v Aqui, R é
Use o teorema de Green para calcular ∫ C F ⋅ d r . (Verifique a orientação da curva antes de aplicar o teorema.) F x , y = y 2 cos ⁡ x , x 2 + 2 y sen ⁡ x C é o triangulo de 0,0 �� ��a ( 2,6 ) a 2,0 a
Se C é o segmento de reta ligando o ponto ( x 1 , y 1 ) ao ponto ( x 2 , y 2 ) , mostre que ∫ C xd y - yd x = x 1 y 2 - x 2 y 1 Se os vértices de um polígono, na ordem anti-horária, são x 1 , y 1 ,x 2
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. ∫ C y + e x d x + 2 x + cos ⁡ y 2 d y C é a fronteira da região englobada pelas parábolas y = x