1. Defina:

1. Assíntotas horizontais.

Vamos dar uma olhada no gráfico da função aqui:

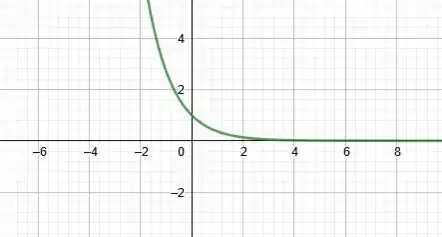
O que será que acontece se a gente colocar um valor de muuuuito grande? Pelo gráfico parece que a nossa função vai praticamente pra zero, né?

Na realidade, o que acontece é que a nossa função fica muito perto de zero, mas nunca chega a encostar no eixo , nesse caso dizemos que o eixo x é uma assíntota de , porque a função chega pertinho do desse eixo, mas nunca encosta nele.

Ou seja, podemos dizer que uma assíntota horizontal nada mais é do que uma reta imaginária que delimita a aproximação de uma função no gráfico à medida que ela cresce ou decresce.

Beleza, mas como a gente resolve se não tivermos o gráfico da função???

Repare que para achar nossa assíntota a gente pensou em pegar um muuuuito grande. Então, o que a gente fez foi basicamente achar o limite da função quando vai pra infinito, olha só:

Maneiro! Chegamos que o nosso limite é igual a zero e o eixo é justamente a reta .

E é assim que a gente consegue achar a assíntota horizontal de qualquer função. Nesse caso aí de cima a gente só jogou pra um valor infinito positivo, só que quando a gente não tem o gráfico o que a gente vai fazer é pegar um muuuuito grande nas duas direções, ou seja, positivo e negativo.

Então, quer dizer que para acharmos uma assíntota horizontal basta a gente resolver dois limites, quando :

Onde .

E quando :

Onde .

Se um ou os dois limites resultarem em um valor finito, ou seja, não explodirem pra mais ou menos infinito, quer dizer que encontramos uma assíntota horizontal.

Só fica atento que não é necessário que os dois limites sejam iguais a uma constante para ser uma assíntota, mas apenas um deles. Caso os dois limites resultem em constantes diferentes, teremos duas assíntotas, uma em cada constante.

Agora vamos para a definição formal. Que é o que o problema pediu, né? Rsrs

Definição: Uma reta é uma assíntota horizontal do gráfico de uma função se

ou

E isso é tudo pessoal. Bora pra próxima.