1. Defina:

1. Assíntotas verticais.

As assíntotas verticais são retas verticais ao qual a nossa função se aproxima sem de fato tocá-las. A função cresce ou decresce infinitamente próxima as assíntotas, como no caso do gráfico da função :

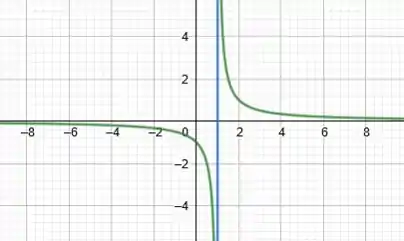
Se a gente olhar com calma quando temos um muuuito grande (tanto positivo quanto negativo) parece que a nossa função praticamente encosta na reta .

Então, isso significa que essa reta é nossa assíntota vertical.

Agora vamos entender o porquê de isso estar acontecendo.

Repare que quando a função chega muito perto de (pela direita e pela esquerda) ela explode pra mais e pra menos infinito. Opa, então o que a gente fez foi, basicamente, resolver esses limites aqui, olha só:

Esse é o lance, o limite de tendendo a algum valor deverá ir para . E esse valor que faz isso com a função será o valor da nossa assíntota. Sacou?!

Mas como a gente descobre que tal valor é esse?

Se olharmos com calma, percebemos que faria nosso denominador resultar zerar, ou seja, daria problema na nossa função. Pois o não está no domínio da nossa função.

Então, para achar as assíntotas verticais, vamos basicamente procurar valores de que não estejam contidos no domínio da função.

Os principais casos que podemos analisar para achar assíntotas verticais são casos onde temos funções quocientes onde o denominador não pode ser zero, funções onde temos raízes de índice par, pois o radicando não pode ser negativo e funções logaritmo onde o argumento não pode ser zero.

Veja outros exemplos:

Para ou nosso denominador zera e se calcularmos o limite de ou , ele irá para .

Assim, e são assíntotas verticais.

Sendo assim, depois de achar esses valores que dão problema na função, a gente resolve o limite com tendendo pra eles tanto pela direita quanto pela esquerda:

Se um desses dois limites explodirem para mais ou para menos infinito, ou seja, se o limite tendendo a pela esquerda ou o limite tendendo a pela direita resultarem em ou , é só partir para o abraço, porque você terá encontrado uma assíntota vertical naquele sentido.

Em resumo, para a gente achar possíveis assíntotas verticais nós temos que:

1. Achar valores de que dão problema na nossa função, ou seja, que não estão no domínio dela (lembrar dos principais casos);
2. Fazer os limites laterais da função com tendendo aos valores problemáticos;
3. Se um desses limites laterais explodirem para mais ou menos infinito, quer dizer que temos uma assíntota vertical;
4. Se os dois limites resultarem em constantes, não temos assíntotas verticais.

Agora vamos para a definição formal. Que é o que o problema pediu, né? Rsrs

Definição: Uma reta é uma assíntota vertical do gráfico de uma função se

ou

E isso é tudo pessoal. Bora pra próxima.