Determine as assíntotas horizontais e verticais, caso existam, da função definida por:
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma função e pediu pra gente encontrar as assíntotas horizontais e verticais. Tá, mas o que são assíntotas mesmo?
Nós podemos dizer que uma assíntota vertical ou horizontal nada mais é do que uma reta imaginária que delimita a aproximação de uma função no gráfico, à medida que essa função cresce ou decresce. Ou seja, quando temos uma função que cresce ou decresce infinitamente e vai se aproximando, chega bem pertinho de um eixo (ou reta), mas sem nunca encostar nele. Tipo assim:
Beleza, mas como é que eu descubro essas assíntotas? Para calcular a assíntota horizontal, a gente precisa pegar um muuuuito grande (ou seja, tendendo pro infinito) nas duas direções, positiva e negativa, e encontrar o limite da função. Então, vamos fazer:
Onde , e nós vamos achar quem é para definir nossa assíntota horizontal. E para as assíntotas verticais? A ideia é parecida, só que nós vamos procurar valores de que podem dar problema no nosso domínio, tipo um denominador que possa dar zero, sabe? Depois de achar esses valores que dão problema na função, a gente resolve os limites com tendendo pra eles tanto pela direita quanto pela esquerda:
Se um desses dois limites derem ou , nós vamos ter encontrado uma assíntota vertical nesse sentido de .
Passo 2
Beleza, vamos começar analisando nossa função:
A gente pode escrever essa função também como um produto de polinômios no numerado e no denominador, assim:
Que é nossa forma fatorada. Cortando os termos semelhantes em cima e embaixo, temos:
Isso vai facilitar pra gente na hora de calcular os limites. Note que mesmo cortando o em cima e embaixo, estaria fora do domínio da função, porque isso faria zerar o denominador original.
Ok, agora vamos procurar nossas assíntotas.
Passo 3
Nós já sabemos pelo passo que assíntotas verticais aparecem onde o domínio não está definido e as horizontais aparecem quando usamos o limite em .
Começando com as verticais, o domínio não está definido em . Então, vamos calcular os limites laterais:
A gente sabe que não existe divisão por zero, então a gente imagina que o denominador chega, na verdade, muito pertinho do zero. Quando isso acontece, a minha função vai pra infinito, mas pro lado negativo, já que ela tá tendendo a pela esquerda. Então,
Agora calculando o limite pela direita, temos:
E dessa vez ela tende a infinito pelo lado positivo, então:
Assim, nós podemos dizer que temos uma assíntota vertical em .
OBS: Repara que também não está no domínio da função original, já que aparece um no denominador de . Porém, o que acontece é que quando calcularmos seu limite para , veremos que ele converge para um valor, e não para , então não constitui uma assíntota vertical. Olha só:
Passo 4
Agora vamos procurar nossas assíntotas horizontais, fazendo o limite de tender para .
Vamos dividir todo mundo por :
Agora percebe que quando for pra infinito, eu vou ter um número constante dividindo outro muito, muito grande? E aí o que acontece é que essa divisão vai pra , porque é como se eu tivesse e . Aí nossa função, depois de aplicada o limite, fica:
E calculando para , fica bem parecido:
Assim, achamos a mesma assíntota horizontal em .
O enuncia não pede o gráfico, mas só pra gente visualizar como ficam nossas assíntotas, elas estão aí em vermelho ( e ):
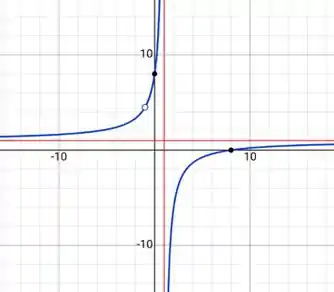
Encerramos o exercício. Valeu, galera! 😉