UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Limites e Continuidade, Questão 5.6
Estude as assíntotas de e esboce seu gráfico.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente encontrar as assíntotas da função e esboçar seu gráfico. Pra isso, a gente precisa lembrar que para encontrar assíntotas horizontais precisamos calcular dois limites:
Onde . Eles não precisam ser iguais, mas se qualquer um desses limites resultar em um valor finito, ou seja, não explodirem para mais ou menos infinito, teremos uma assíntota horizontal.
E pra verificar se a função tem assíntotas verticais, precisamos olhar para os valores que não estão definidos no domínio da função. No nosso caso, para , teríamos , ou seja, uma indeterminação. Dessa forma, nós calculamos os limites laterais nesse ponto:
Se eles explodirem para mais ou menos infinitos, teremos assíntotas verticais nesse ponto.
Vamos lá!
Passo 2
Vamos começar verificando as assíntoas horizontais da função, calculando o limite:
Dividindo todo mundo por , temos:
Quando , as frações com no denominador tendem a zero. Logo, temos:
Agora para , temos da mesma forma:
Portanto, temos uma assíntota horizontal em .
Passo 3
Agora verificando a existência de assíntotas verticais, vamos calcular:
Para se aproximando de pela direita, e temos um denominador positivo que se aproxima de zero, . Dessa forma,
Agora para o limite lateral pela esquerda, temos:
Para se aproximando de pela esquerda, e temos um denominador negativo que se aproxima de zero, . Dessa forma,
Como os limites laterais para explodem para infinito, temos uma assíntota vertical em .
Esboçando o gráfico da função, temos:
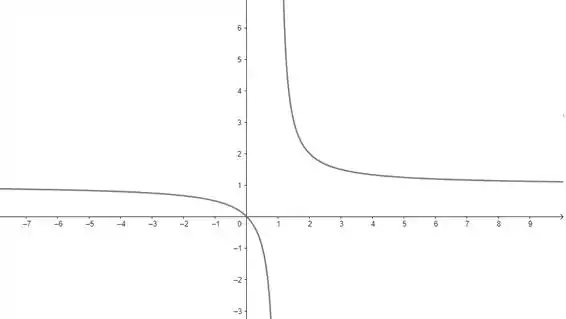
Valeu, galera! Até a próxima! 😉