UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 4.3.1f
Seja uma função definida em , contínua em todo o seu domínio e satisfazendo as condições abaixo:
e
Suponha que o gráfico de é dado pela figura abaixo:
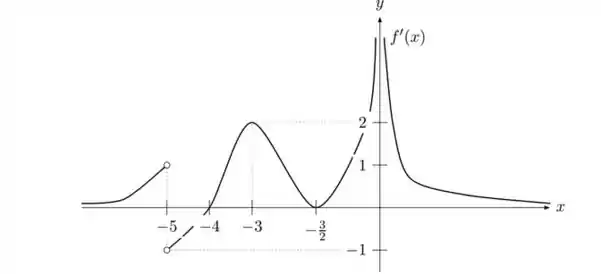
Responda, justificando, o que se pede:
As assíntotas verticais e horizontais, caso existam;
Passo 1
Olá pessoal, como estão?
Nessa questão temos uma função , com a informação de algum dos seus pontos:
Também foi dado o gráfico da derivada de , ou seja,
Além disso, o enunciado também nos falou que:
Nesse item precisamos determinar as assíntotas verticais e horizontais de .
Para fazer isso, basta analisarmos o gráfico quando se tende a algum valor constante (assíntotas horizontais), e se tem tende a infinito antes e depois de um certo valor de fixo de (assíntota vertical).
Vem com a gente que vai ficar mais claro!
Passo 2
Bom, vamos começar pensando nas assíntotas horizontais...
Foi dado no enunciado, que:
Isso significa que, quando , assume um valor constante, que é o valor nulo. Ou seja, à medida que aumenta em módulo, a curva se aproxima do eixo .
Portanto, temos uma assíntota horizontal em .
Já na assíntota vertical, vamos analisar o gráfico:
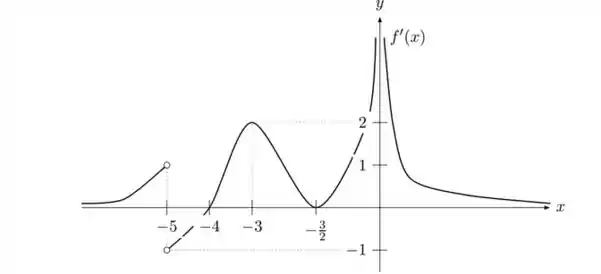
Olha junto comigo, à medida que se aproxima de , a nossa função derivada explode pro infinito. Isso significa, na função primitiva , que quando ela se aproxima de , o seu valor aumenta absurdamente, sem que a função nunca realmente alcance a reta .
Ou seja, é uma assíntota vertical.
E é isso galera! Pegaram a ideia?
Valeu pela atenção!
Resposta
assíntota vertical
assíntota horizontal