UTFPR, Pato Branco, Cálculo Diferencial e Integral 1, AV3 - 2023.1
Calcule o volume do solido obtido pela rotação da região limitada pelas curvas e , em torno do eixo x, no intervalo [0,1].
Passo 1
Olá meu caro amigo, espero que você esteja bem e super dispostos a aprender um pouco mais hoje. Que tal responder comigo essa querida integral?
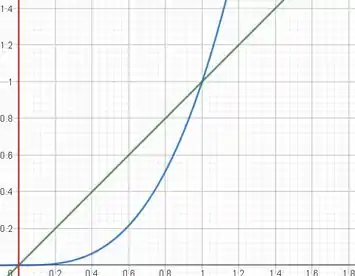
Passo 2
Iremos colocar para girar a região delimitada pelas linhas verde e azul, isso em torno do eixo x. O volume é dado por
Em nosso caso, como temos duas equações, a nossa integração será,
E assim terminamos nossa prova, espero que tenha sanado suas duvidas e um forte abraço.
Resposta
Exercícios de Livros Relacionados
58. A base de S é a região delimitada pela parábola y = 1 - x 2 e pelo eixo x . As secções transversais perpendiculares ao eixo y são quadradas.
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Esboce uma casca cilíndrica típica e encontre sua circunferência e altura. Use cascas para encontrar o volume
Use os resultados desta seção para deduzir o Princípio de Cavalieri (Exercício 64 ).
Conforme a figura abaixo, a cúpula de uma catedral foi projetada com três suportes semicirculares de raio r , de modo que cada seção transversal horizontal é um hexágono regular. Mostre que o volume d