Calcule o volume do sólido obtido pela rotação, em torno da reta , da região limitada pelas curvas e , para .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar o volume do sólido gerado pela rotação, em torno da reta , da região limitada pelas curvas , , e . Mas que região é essa? Vamos dar uma olhadinha no gráfico:
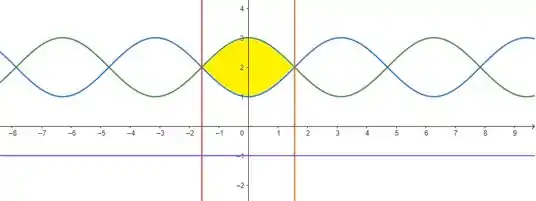
Nossa região é essa aí em amarelo e é ela que vai girar em torno da reta em lilás. Nesse caso, temos duas curvas girando em torno de uma reta paralela ao eixo , quando isso acontece precisamos considerar que os raios de rotação, externo e interno , são dados pelas distâncias de cada curva até o eixo de revolução, que aqui é . Sendo assim, vamos ter:
E a nossa integral de volume, vai ser dada por:
Então, vamos substituir os raios e calcular a integral. Vamos lá!
Passo 2
Conforme vimos no passo anterior, vamos ter:
Substituindo as funções no integrando junto com o eixo de revolução, no intervalo , temos:
Expandindo esses produtos notáveis, vai ficar:
Simplificando:
Colocando a constante pra fora da integral:
Integrando:
Aplicando os intervalos de integração:
Encontramos nosso volume.
Valeu, galera! Até a próxima! 😉