UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 6.2.4
Considere o sólido gerado pela rotação, em torno do eixo , da região limitada pela parábola e a reta , com . Determine o valor de se o volume deste sólido é .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente considerar o sólido gerado pela rotação, em torno do eixo , da região limitada pela parábola e a reta , com e determinar o valor de . Mas que região é essa? Bom, se a gente considerar , vamos ter isso aqui:
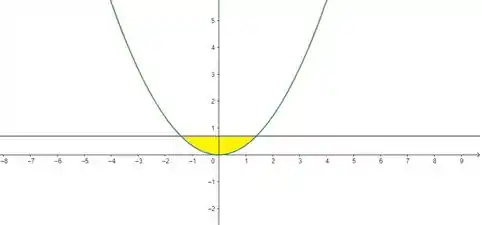
Como é sempre positivo (), o que pode mudar no gráfico é a reta ser mais pra cima e a parábola ser mais aberta ou mais fechada. Mas de qualquer forma, a gente consegue visualizar a região, o que é importante.
Nós sabemos que e vão girar em torno do eixo e gerar um sólido de volume . Quando duas curvas giram em torno do eixo , nós precisamos considerar que o volume do sólido será dado pela diferença entre o volume da região maior, de raio , e o volume da região menor, de raio . Sendo assim, temos:
No nosso caso, é a função que está por cima, , e é a função que está abaixo, . Então, vamos substituir os dados calcular a integral. Vamos lá!
Passo 2
Antes de substituir os raios e o volume na integral, vamos encontrar o intervalo de integração , igualando as equações das curvas:
Tirando a raiz dos dois lados:
Então, nosso intervalo será . Substituindo tudo na integral de volume, temos:
Repare que é uma constante e a gente integra em relação a . Então, vamos ter:
Aplicando os intervalos de integração:
Mas o enunciado nos diz que . Então, temos:
Isolando e tirando a raiz cúbica:
Valeu, galera! Até a próxima! 😉