UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 6.2.7
Encontre o volume do sólido obtido pela rotação, em torno do eixo , da região infinita situada entre o gráfico de e sua assíntota horizontal.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular o volume de rotação, em torno do eixo , da região limitada pela curva e e sua assíntota horizontal. Mas que região é essa? Vamos dar uma olhadinha no gráfico:
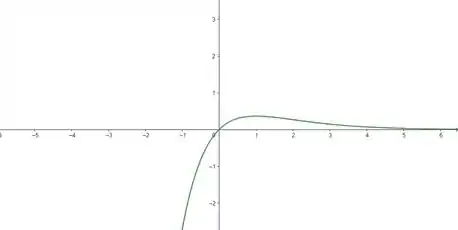
Repare que sua assíntota horizontal é o eixo (), porque a curva vai se aproximando cada vez mais dele, mas nunca realmente toca o eixo, e justamente por isso, nossa região é infinita. Isso significa que nosso limite de integração vai de até . Além disso, a gente precisa lembrar que nosso volume de rotação é dado pela integral:
Assim, substituindo os dados do enunciado, conseguimos obter o volume do sólido gerado.
Vamos lá!
Passo 2
Sabendo que , no intervalo , vamos ter:
Elevando ao quadrado:
Como temos um produto difícil de integrar, vamos usar a integração por partes para facilitar nossa vida (). Chamando:
Substituindo na fórmula da integral por partes:
A gente continua com um produto difícil de resolver no integrando, então vamos aplicar a integral por parte de novo. Dessa vez, fazendo:
Substituindo na fórmula, junto com o resultado de cima, fica:
Agora sim, integrando, temos:
Colocando em evidência e tirando o M.M.C.:
Para o limite superior, precisamos calcular o limite de quando . No limite inferior, apenas substituímos . Voltando a fórmula do volume, fica assim:
Quando , vamos ter . Então, nosso resultado será:
Valeu, galera! Até a próxima! 😉